Hạ bậc cos mũ 3
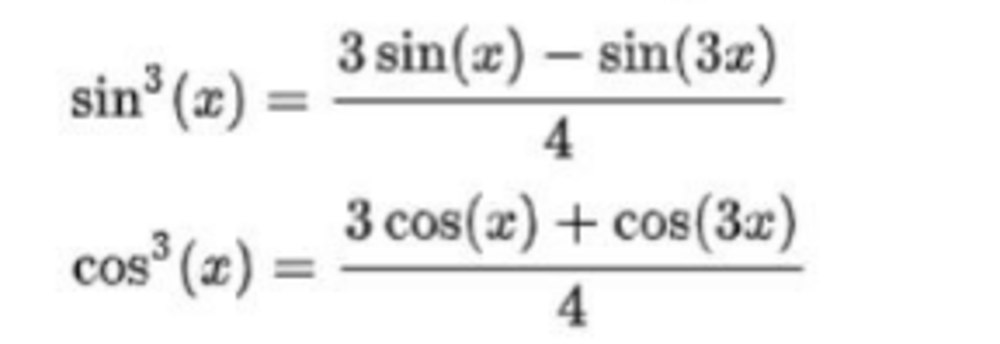
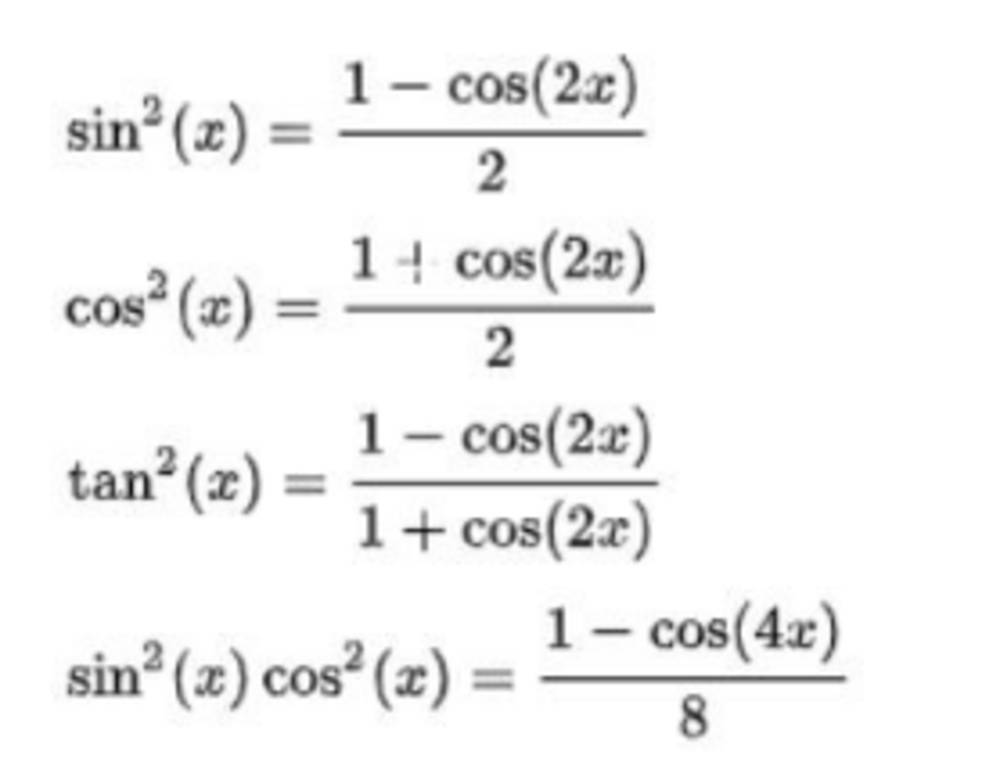
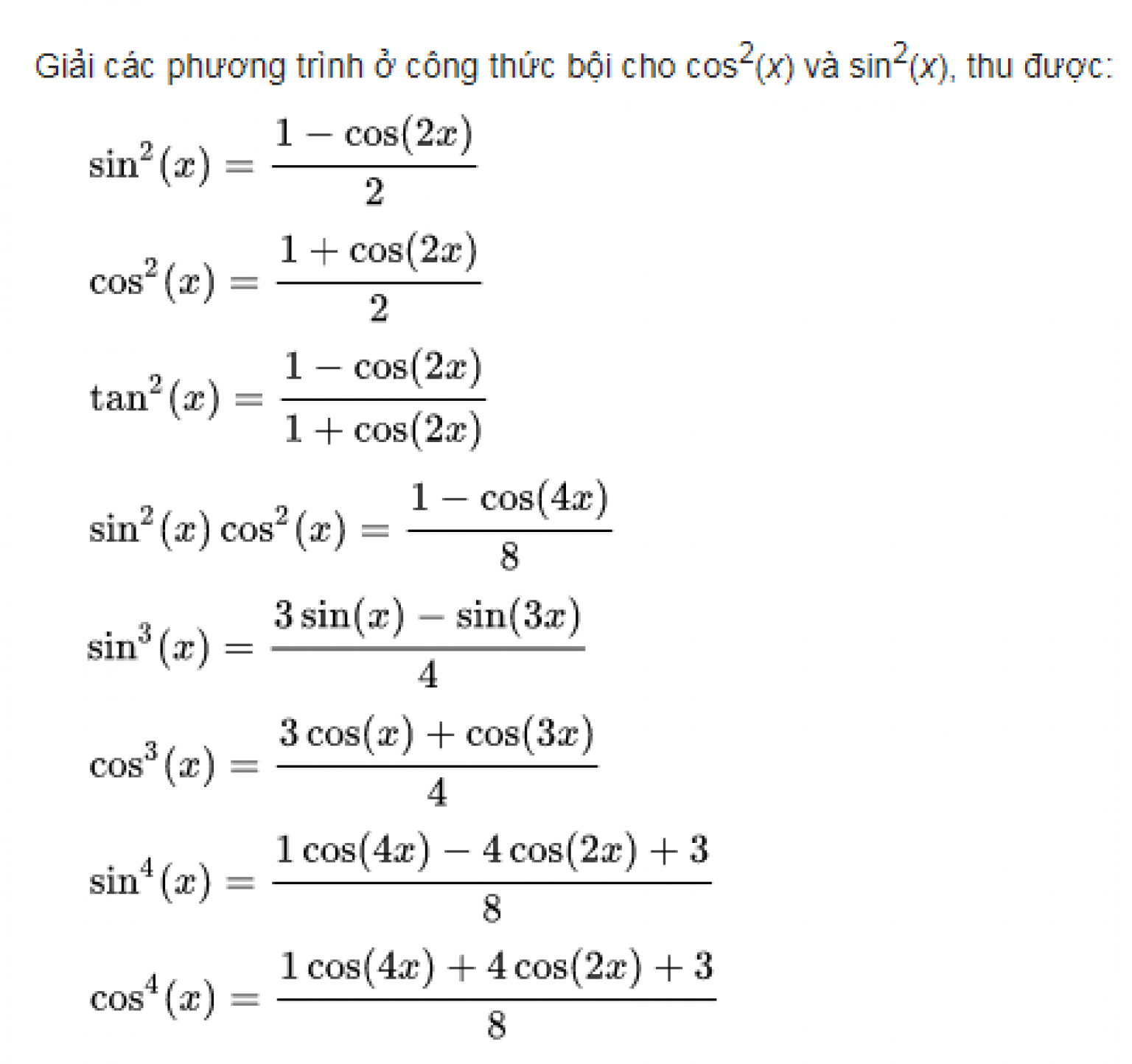
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Công thức hạ bậc cos mũ 3 là: cos³x = (1/4)(3cosx + cos3x). Công thức này giúp biến đổi biểu thức chứa cos³x thành dạng đơn giản hơn, thuận tiện hơn trong việc tính toán và giải phương trình lượng giác. Dưới đây là chi tiết cách chứng minh và ví dụ áp dụng.
Chứng minh công thức hạ bậc cos mũ 3
Sử dụng công thức cộng
Ta có công thức cos(3x) = 4cos³x - 3cosx. Từ đây, ta có thể biến đổi để tìm cos³x:
cos(3x) + 3cosx = 4cos³x
cos³x = (1/4)(cos(3x) + 3cosx)
Vậy, công thức hạ bậc cos mũ 3 được chứng minh.
Sử dụng công thức lượng giác
Một cách chứng minh khác là sử dụng công thức cos(a+b) và cos(a-b) để biểu diễn cos³x thành tổng của các hàm cos với bậc thấp hơn. Tuy nhiên, phương pháp này phức tạp hơn và ít được sử dụng.
Ứng dụng của công thức hạ bậc cos mũ 3
Giải phương trình lượng giác
Công thức này rất hữu ích trong việc giải các phương trình lượng giác phức tạp. Bằng cách hạ bậc cos³x xuống thành các hàm cos với bậc thấp hơn, ta có thể đưa phương trình về dạng dễ giải hơn.
Tính tích phân
Trong tính toán tích phân, việc hạ bậc cos³x giúp đơn giản hóa tích phân và dễ dàng tìm được kết quả.
Đơn giản hóa biểu thức
Công thức này giúp đơn giản hóa các biểu thức lượng giác phức tạp, làm cho việc tính toán và phân tích trở nên dễ dàng hơn.
Như vậy, công thức hạ bậc cos mũ 3 là một công cụ quan trọng trong lượng giác, giúp giải quyết nhiều bài toán phức tạp một cách hiệu quả.
Xem thêm: quê tôi như thuở nào
Sản phẩm liên quan: nước tràn bờ đê
Sản phẩm hữu ích: bao lâu thì cây lưỡi hổ ra hoa