Góc Đặc Biệt Trong Lượng Giác: Hướng Dẫn Chi Tiết và Ứng Dụng

Mô tả sản phẩm

Góc đặc biệt trong lượng giác là những góc có giá trị lượng giác (sin, cos, tan, cot) được tính toán chính xác và thường được sử dụng rộng rãi trong các bài toán. Bài viết này sẽ giúp bạn hiểu rõ hơn về các góc đặc biệt này, cách tính giá trị lượng giác của chúng và ứng dụng trong thực tế.

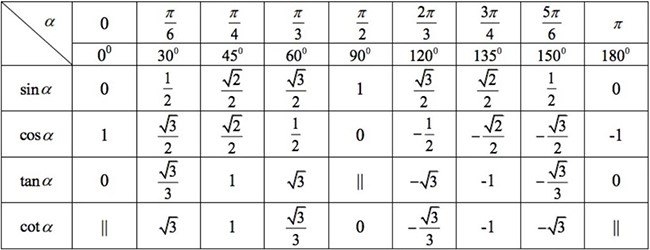
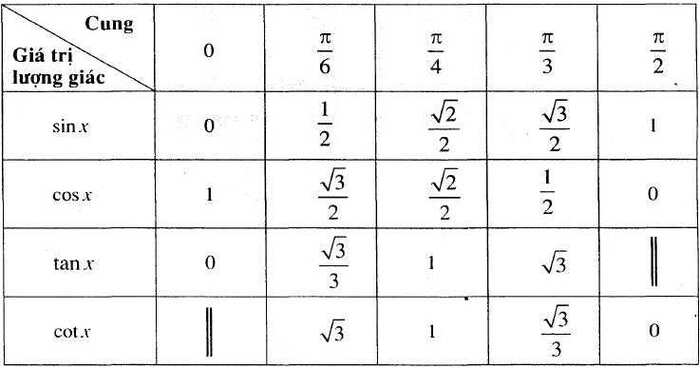
Các Góc Đặc Biệt Thường Gặp

Góc 0°, 30°, 45°, 60°, 90° và các bội của chúng

Những góc này có giá trị lượng giác rất dễ nhớ và thường xuyên xuất hiện trong các bài toán lượng giác cơ bản. Bạn cần nắm vững bảng giá trị lượng giác của các góc này để giải quyết nhanh chóng và chính xác các bài tập. Ví dụ: sin 30° = 1/2, cos 60° = 1/2, tan 45° = 1, v.v... Việc ghi nhớ bảng này sẽ giúp bạn tiết kiệm thời gian đáng kể trong quá trình học tập và làm bài.

Góc 180°, 270°, 360° và các bội của chúng

Đây là những góc đặc biệt quan trọng khác, đại diện cho các vị trí đặc biệt trên đường tròn lượng giác. Hiểu rõ giá trị lượng giác của các góc này giúp bạn dễ dàng xác định các góc đồng dạng và rút gọn các biểu thức lượng giác phức tạp.

Ứng Dụng của Góc Đặc Biệt Trong Lượng Giác

Giải Phương Trình Lượng Giác

Việc nắm vững giá trị lượng giác của các góc đặc biệt là rất cần thiết khi giải phương trình lượng giác. Bạn có thể sử dụng các giá trị này để tìm nghiệm của phương trình và xác định các nghiệm trong khoảng cho trước.

Tính Toán Trong Hình Học

Trong hình học, các góc đặc biệt được sử dụng rộng rãi để tính toán các cạnh, góc và diện tích của các hình tam giác, hình vuông, hình chữ nhật, v.v... Ví dụ, trong tam giác vuông, bạn có thể sử dụng các tỷ số lượng giác để tính độ dài các cạnh khi biết một góc đặc biệt và một cạnh.

Ứng Dụng trong Vật Lý và Kỹ Thuật

Góc đặc biệt cũng đóng vai trò quan trọng trong nhiều lĩnh vực của vật lý và kỹ thuật, chẳng hạn như cơ học, điện tử và quang học. Việc hiểu rõ về các góc đặc biệt giúp bạn phân tích và giải quyết các bài toán liên quan đến chuyển động, sóng và dao động.

Xem thêm: dòng điện xoay chiều là gì cách tạo ra dòng điện xoay chiều

Sản phẩm liên quan: cây xương khỉ là cây gì

Sản phẩm liên quan: diện tích hình thang có 2 góc vuông