Đường tròn nội tiếp tam giác là giao điểm của

Mô tả sản phẩm

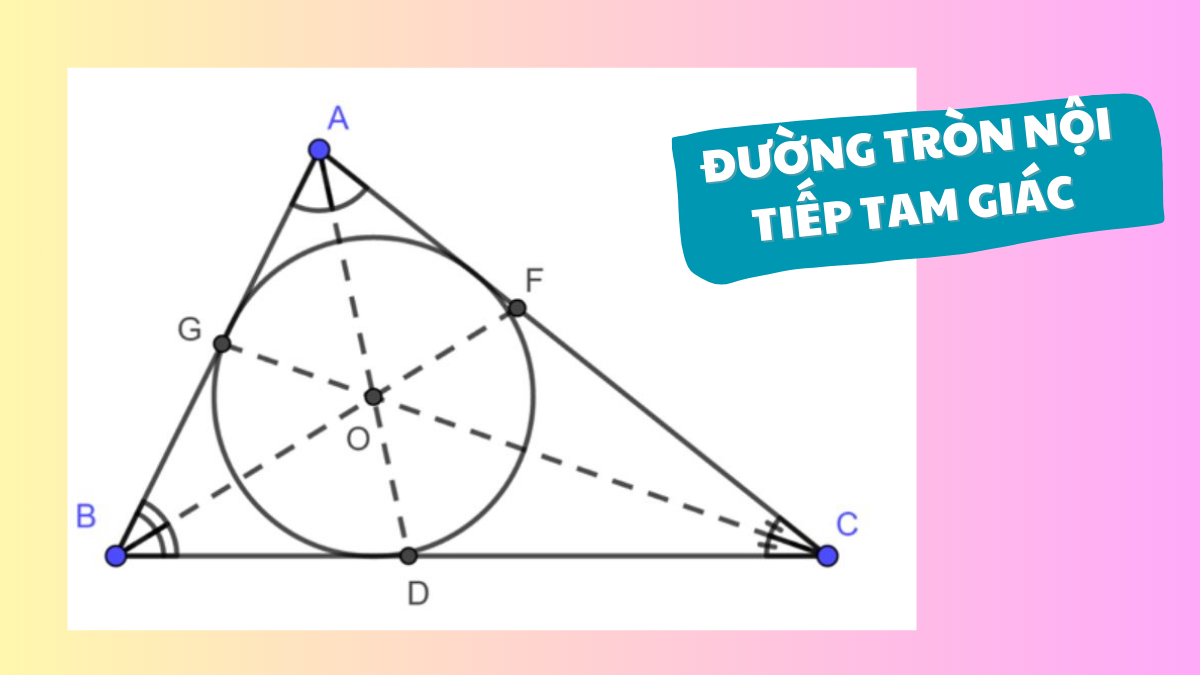
Đường tròn nội tiếp tam giác là giao điểm của ba đường phân giác trong của tam giác đó. Cụ thể hơn, tâm của đường tròn nội tiếp (gọi là tâm nội tiếp) là giao điểm của ba đường phân giác, và bán kính của đường tròn nội tiếp là khoảng cách từ tâm nội tiếp đến mỗi cạnh của tam giác.

Tính chất của đường tròn nội tiếp tam giác

Tâm nội tiếp và bán kính

Tâm của đường tròn nội tiếp tam giác được ký hiệu là I. Điểm I là giao điểm của ba đường phân giác trong của tam giác. Bán kính của đường tròn nội tiếp, ký hiệu là r, được tính bằng công thức r = S/p, trong đó S là diện tích tam giác và p là nửa chu vi tam giác (p = (a+b+c)/2, với a, b, c là độ dài ba cạnh của tam giác).

Liên hệ với các yếu tố khác của tam giác

Đường tròn nội tiếp luôn nằm hoàn toàn bên trong tam giác. Tâm nội tiếp I luôn nằm trong tam giác. Bán kính đường tròn nội tiếp có mối liên hệ chặt chẽ với diện tích và chu vi của tam giác. Ngoài ra, đường tròn nội tiếp còn có nhiều tính chất liên quan đến các đường cao, trung tuyến, và đường trung trực của tam giác.

Ứng dụng của đường tròn nội tiếp tam giác

Trong giải toán hình học

Hiểu rõ về đường tròn nội tiếp giúp giải quyết nhiều bài toán hình học phức tạp liên quan đến tính toán diện tích, chu vi, các góc và các cạnh của tam giác. Việc xác định tâm nội tiếp và bán kính đường tròn nội tiếp là bước quan trọng trong việc giải quyết nhiều bài toán.

Trong thiết kế và xây dựng

Ứng dụng của đường tròn nội tiếp cũng được thấy trong các lĩnh vực thiết kế và xây dựng. Ví dụ, trong việc thiết kế các cấu trúc hình học, việc sử dụng đường tròn nội tiếp có thể giúp tối ưu hóa diện tích và tạo ra các hình dạng cân đối và hài hòa.

Sản phẩm hữu ích: cặp học sinh lớp 1 cho be trai

Xem thêm: ôn tập cuối kì 2 lớp 3

Sản phẩm hữu ích: dẫn hỗn hợp khí gồm co2 co so2 lội qua dung dịch nước vôi trong dư khí thoát ra là

Sản phẩm hữu ích: chành xe anh tuấn

Xem thêm: nước gia ven là gì