Đường Tròn Lượng Giác Là Gì?

Mô tả sản phẩm

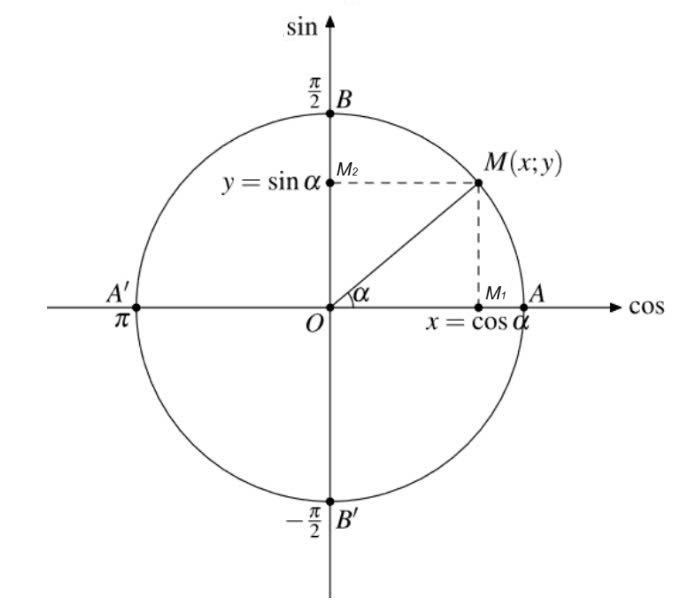
Đường tròn lượng giác là một hình tròn có bán kính bằng 1 đơn vị, được sử dụng để biểu diễn các giá trị lượng giác của một góc. Nó giúp trực quan hóa mối quan hệ giữa các hàm lượng giác như sin, cos, tan và cot.

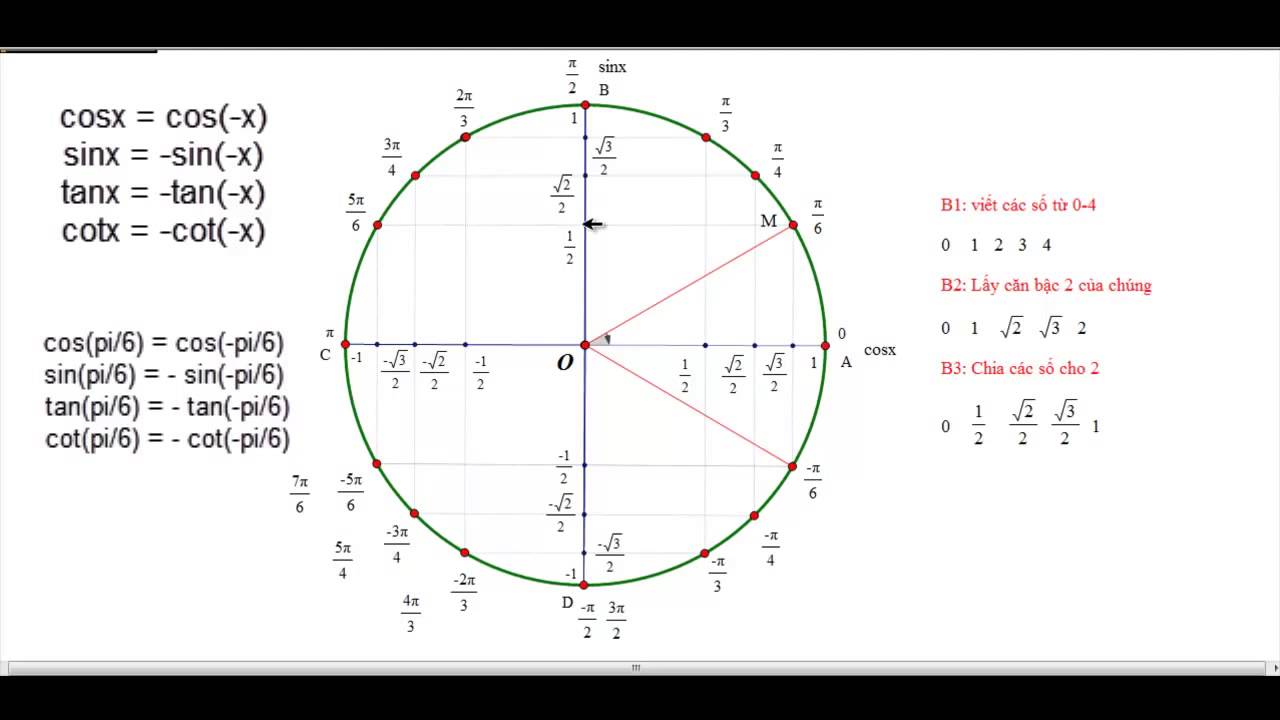
Cấu tạo và cách sử dụng đường tròn lượng giác

Hệ trục tọa độ và các điểm đặc biệt:

Đường tròn lượng giác được vẽ trên hệ trục tọa độ Oxy, với tâm là gốc tọa độ O(0;0) và bán kính bằng 1. Trên đường tròn, ta đánh dấu các điểm đặc biệt tương ứng với các góc tiêu biểu như 0, π/6, π/4, π/3, π/2, π, 3π/2, 2π… Mỗi điểm trên đường tròn đại diện cho một góc xác định.

Biểu diễn các giá trị lượng giác:

Cho một góc α bất kỳ, ta xác định điểm M trên đường tròn lượng giác tương ứng với góc α. Tọa độ của điểm M (x; y) sẽ cho ta các giá trị lượng giác: x = cos α và y = sin α. Từ đó, ta dễ dàng tính được tan α = y/x và cot α = x/y (khi x ≠ 0).

Ứng dụng của đường tròn lượng giác

Đường tròn lượng giác được ứng dụng rộng rãi trong nhiều lĩnh vực, đặc biệt là toán học và vật lý. Nó giúp giải quyết các bài toán liên quan đến:

Giải phương trình lượng giác:

Đường tròn lượng giác giúp ta tìm nghiệm của phương trình lượng giác một cách trực quan và dễ hiểu hơn.

Xác định dấu của các hàm lượng giác:

Nhờ đường tròn lượng giác, ta có thể dễ dàng xác định dấu của sin, cos, tan và cot trong từng góc phần tư.

Nghiên cứu tính tuần hoàn của hàm lượng giác:

Tính chất tuần hoàn của các hàm lượng giác được thể hiện rõ ràng trên đường tròn lượng giác. Tóm lại, đường tròn lượng giác là một công cụ trực quan và hiệu quả để hiểu và ứng dụng các kiến thức về lượng giác. Nó đơn giản hóa việc giải quyết các bài toán phức tạp và giúp chúng ta nắm bắt tốt hơn mối quan hệ giữa các hàm lượng giác.

Sản phẩm hữu ích: n trong youtube la gì

Sản phẩm liên quan: công thức tính điện tích hạt nhân

Sản phẩm liên quan: công dụng của bản vẽ lắp là

Sản phẩm liên quan: công nghệ lớp 3 cánh diều

Sản phẩm liên quan: số âm cộng số âm ra gì