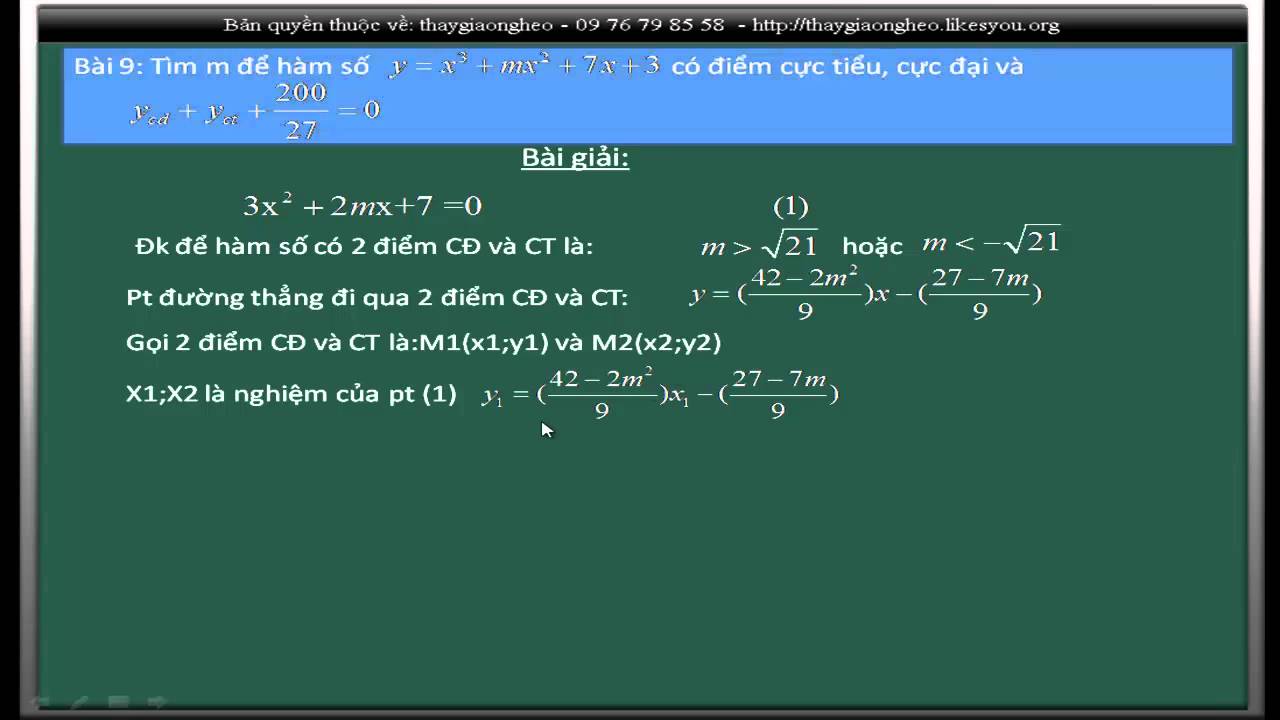
Đường thẳng đi qua 2 điểm cực trị

Mô tả sản phẩm

Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = f(x) thường được biểu diễn dưới dạng y = ax + b, trong đó a và b là các hệ số cần xác định. Việc tìm phương trình đường thẳng này giúp ta phân tích và hiểu rõ hơn về đồ thị hàm số, đặc biệt là vị trí và tính chất của các điểm cực trị.

Phương pháp tìm đường thẳng đi qua 2 điểm cực trị

Tìm tọa độ điểm cực trị

Để tìm phương trình đường thẳng đi qua hai điểm cực trị, trước hết ta cần tìm tọa độ của các điểm cực trị. Điều này được thực hiện bằng cách tính đạo hàm bậc nhất của hàm số f'(x), giải phương trình f'(x) = 0 để tìm các điểm cực trị x₁, x₂,... Sau đó, thay các giá trị x₁, x₂,... vào hàm số ban đầu f(x) để tìm các giá trị y tương ứng y₁, y₂,... Tọa độ các điểm cực trị sẽ là (x₁, y₁), (x₂, y₂),...

Xác định phương trình đường thẳng

Sau khi tìm được tọa độ ít nhất hai điểm cực trị (x₁, y₁) và (x₂, y₂), ta có thể sử dụng công thức phương trình đường thẳng đi qua hai điểm: hoặc sử dụng phương trình tổng quát: với A, B, C là các hệ số cần xác định. Tuy nhiên, trong nhiều trường hợp, việc sử dụng phương pháp đạo hàm và chia đa thức sẽ đơn giản hơn.

Phương pháp đạo hàm và chia đa thức

Đối với các hàm số đa thức, ta có thể sử dụng phương pháp đạo hàm và chia đa thức. Cụ thể, ta chia đa thức f(x) cho f''(x) (đạo hàm bậc hai của f(x)) để tìm thương và dư. Phần thương chính là phương trình đường thẳng đi qua hai điểm cực trị. Phương pháp này dựa trên lý thuyết về phép chia đa thức và mối liên hệ giữa đạo hàm bậc nhất và bậc hai của hàm số.

Sản phẩm hữu ích: duong giua toan nang

Sản phẩm liên quan: sách luyện thi ket

Sản phẩm liên quan: định nghĩa nguyên tố hóa học