Định Lý Tam Giác Đều

Mô tả sản phẩm

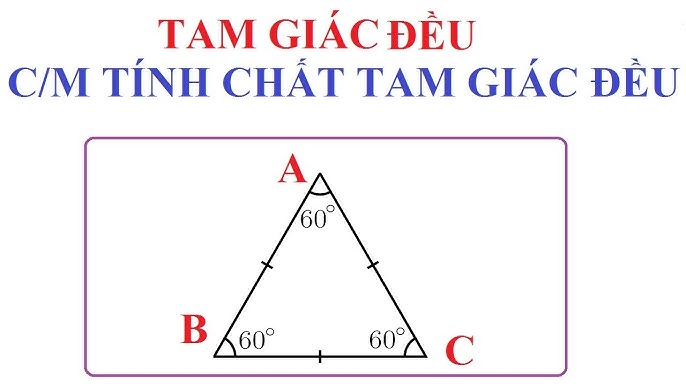
Định lý tam giác đều khẳng định rằng một tam giác có ba cạnh bằng nhau thì ba góc của nó cũng bằng nhau và bằng 60 độ. Ngược lại, nếu một tam giác có ba góc bằng nhau và bằng 60 độ thì ba cạnh của nó cũng bằng nhau.

Tính chất của tam giác đều

Ba cạnh bằng nhau:

Đây là tính chất cơ bản và là định nghĩa của tam giác đều. Tất cả ba cạnh của tam giác đều có độ dài bằng nhau.

Ba góc bằng nhau:

Mỗi góc trong tam giác đều đều có số đo bằng 60 độ. Tổng ba góc trong một tam giác luôn bằng 180 độ, và trong tam giác đều, mỗi góc đóng góp 60 độ vào tổng này.

Trung tuyến, đường cao, đường trung trực trùng nhau:

Trong tam giác đều, đường trung tuyến, đường cao và đường trung trực xuất phát từ cùng một đỉnh sẽ trùng nhau. Điều này dẫn đến nhiều tính chất quan trọng khác.

Đường phân giác:

Đường phân giác của mỗi góc trong tam giác đều cũng là đường trung tuyến, đường cao và đường trung trực.

Tính đối xứng:

Tam giác đều có tính đối xứng cao, nó có 3 trục đối xứng, mỗi trục đi qua một đỉnh và trung điểm của cạnh đối diện.

Công thức liên quan đến tam giác đều

Diện tích:

Diện tích của tam giác đều với cạnh a được tính bằng công thức: S = (a²√3)/4

Chu vi:

Chu vi của tam giác đều với cạnh a là: P = 3a

Bán kính đường tròn ngoại tiếp:

Bán kính đường tròn ngoại tiếp tam giác đều với cạnh a là: R = a/(√3)

Bán kính đường tròn nội tiếp:

Bán kính đường tròn nội tiếp tam giác đều với cạnh a là: r = (a√3)/6

Ứng dụng của tam giác đều

Tam giác đều có nhiều ứng dụng trong thực tiễn và trong các lĩnh vực khác nhau như: kiến trúc (thiết kế các cấu trúc bền vững), nghệ thuật (tạo nên các họa tiết đối xứng), kỹ thuật (trong thiết kế cơ khí và máy móc). Hình dạng đối xứng và tính chất đặc biệt của tam giác đều làm cho nó trở thành một hình học lý tưởng trong nhiều ứng dụng.

Sản phẩm liên quan: phiếu bài tập tiếng việt

Sản phẩm hữu ích: con chó tô màu gì

Sản phẩm hữu ích: v cut là gì

Sản phẩm liên quan: mua naoh ở đâu

Sản phẩm hữu ích: h là trực tâm của tam giác abc