Định Lý Hình Thoi

Mô tả sản phẩm

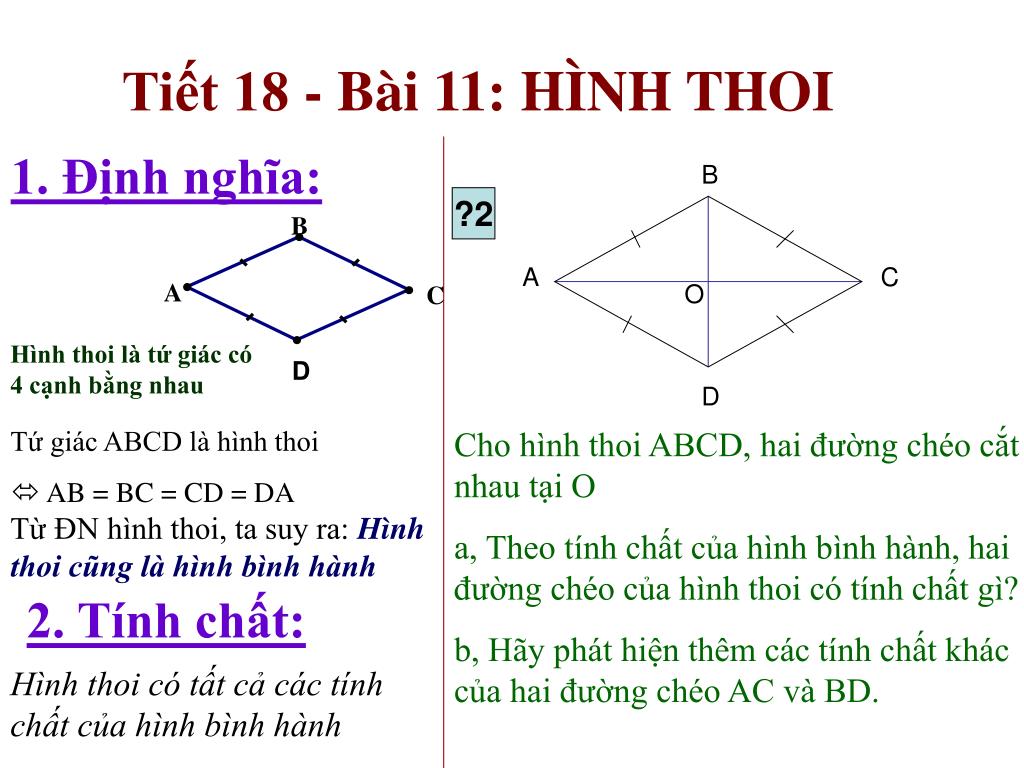
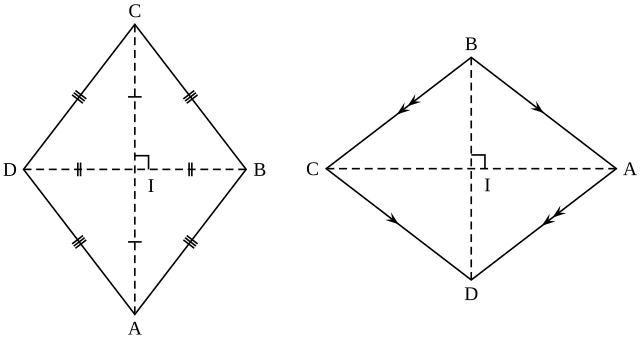
Định lý hình thoi khẳng định rằng: Hai đường chéo của hình thoi vuông góc với nhau và cắt nhau tại trung điểm mỗi đường. Điều này có nghĩa là nếu bạn vẽ hai đường chéo trong một hình thoi, chúng sẽ tạo thành bốn góc vuông và điểm giao nhau sẽ chia đôi mỗi đường chéo.

Các thuộc tính quan trọng của hình thoi

Các cạnh bằng nhau:

Tất cả các cạnh của hình thoi đều có độ dài bằng nhau. Đây là đặc điểm cơ bản phân biệt hình thoi với các hình tứ giác khác.

Các góc đối bằng nhau:

Hai góc đối diện trong hình thoi luôn có số đo bằng nhau.

Các đường chéo vuông góc:

Như định lý đã nêu, hai đường chéo của hình thoi luôn vuông góc với nhau, tạo thành bốn góc vuông tại điểm giao nhau.

Các đường chéo là đường phân giác:

Mỗi đường chéo của hình thoi là đường phân giác của hai góc đối diện mà nó đi qua. Điều này có nghĩa là nó chia đôi mỗi góc đó thành hai góc bằng nhau.

Ứng dụng của định lý hình thoi:

Định lý hình thoi có nhiều ứng dụng trong toán học và các lĩnh vực khác, ví dụ như:

• Tính toán diện tích hình thoi: Diện tích hình thoi bằng một nửa tích độ dài hai đường chéo.
• Xác định các mối quan hệ giữa các cạnh và góc trong hình thoi.
• Giải các bài toán hình học phức tạp hơn liên quan đến hình thoi.

Hiểu rõ định lý hình thoi và các thuộc tính của nó là rất quan trọng để giải quyết các bài toán hình học liên quan đến hình thoi một cách hiệu quả. Việc nắm vững định lý này sẽ giúp bạn dễ dàng hơn trong việc tính toán, chứng minh và ứng dụng trong các bài toán thực tế.

Sản phẩm liên quan: tranh tô màu nghề nghiệp cho bé

Sản phẩm liên quan: bán kính nguyên tử phụ thuộc vào yếu tố nào

Sản phẩm hữu ích: tinh chat hinh thoi

Xem thêm: al + o2 = al2o3