Định Lý Cosin Trong Tam Giác Thường

Mô tả sản phẩm

Định lý Cosin trong tam giác thường giúp ta tính độ dài một cạnh của tam giác nếu biết độ dài hai cạnh còn lại và góc xen giữa chúng. Hay nói cách khác, nó liên hệ giữa độ dài các cạnh và góc của một tam giác bất kỳ.

Công thức Định Lý Cosin

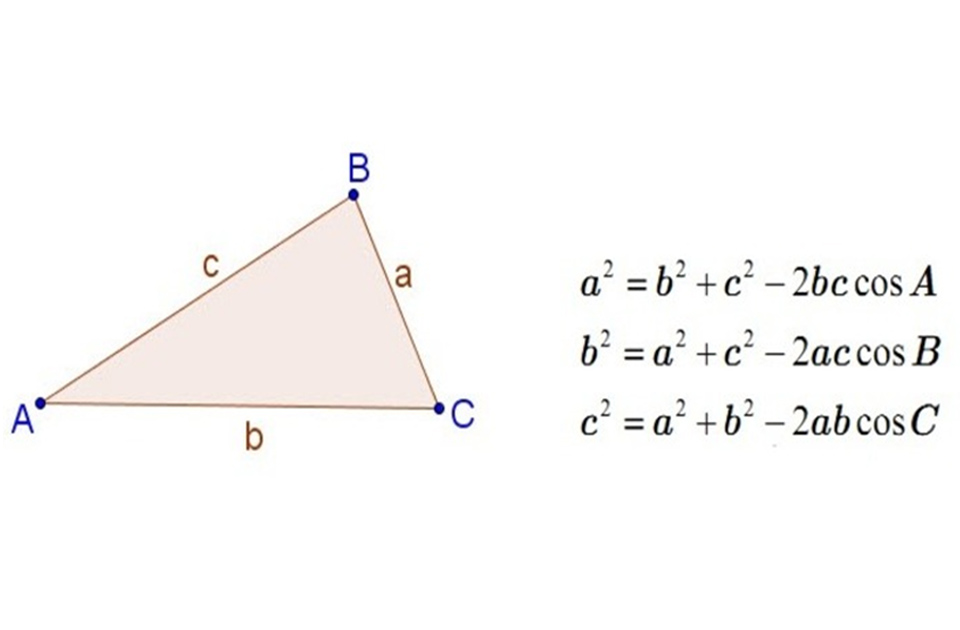
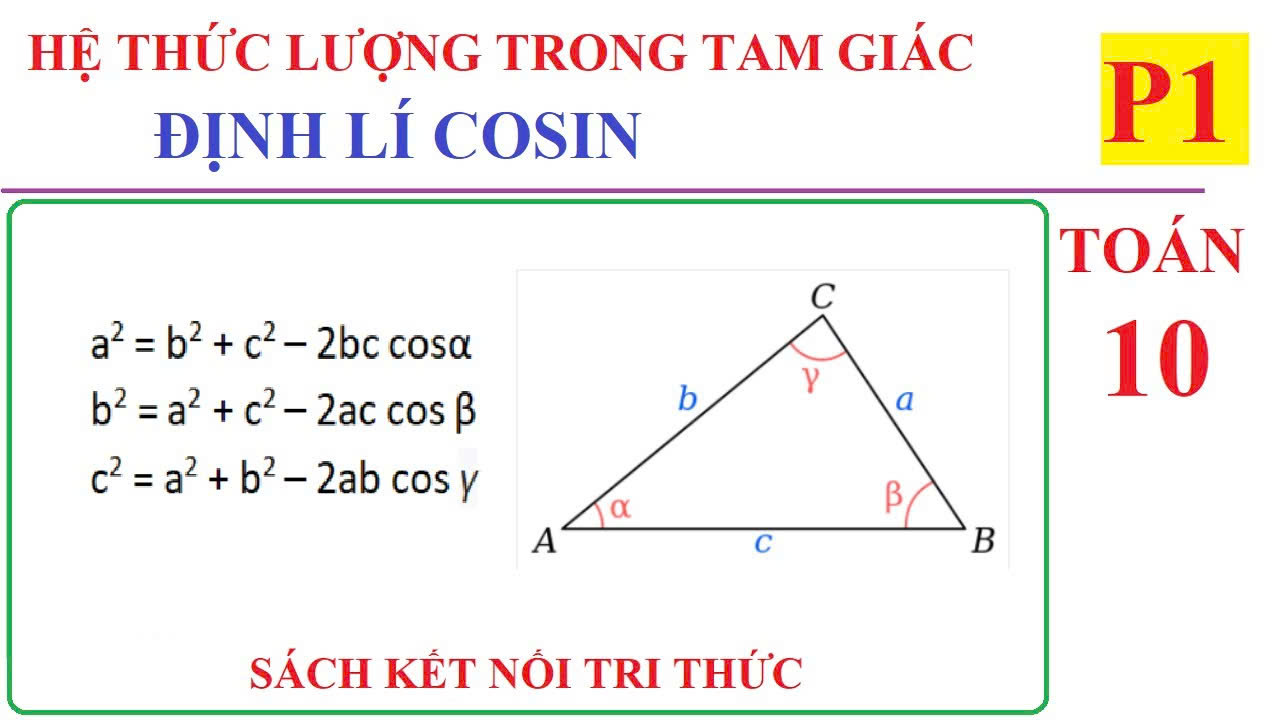
Trong tam giác ABC, với a, b, c lần lượt là độ dài các cạnh đối diện với các góc A, B, C, ta có:

• a² = b² + c² - 2bc.cosA
• b² = a² + c² - 2ac.cosB
• c² = a² + b² - 2ab.cosC

Ứng dụng của Định Lý Cosin

Định lý Cosin có nhiều ứng dụng quan trọng trong toán học và các lĩnh vực liên quan, chẳng hạn như:

• Giải tam giác: Tính độ dài cạnh và góc của tam giác khi biết một số dữ kiện khác.
• Hình học phẳng: Chứng minh các tính chất hình học, giải các bài toán liên quan đến tam giác.
• Vật lý: Áp dụng trong việc tính toán quãng đường, vận tốc, gia tốc.
• Kỹ thuật: Sử dụng trong thiết kế, xây dựng, đo đạc.

Ví dụ minh họa

Giả sử ta có tam giác ABC với AB = 5cm, BC = 7cm và góc B = 60°. Để tính độ dài cạnh AC (hay a), ta áp dụng công thức:

a² = b² + c² - 2bc.cosA
Tuy nhiên, trong trường hợp này ta biết cạnh b, c và góc B, nên ta dùng công thức:

a² = b² + c² - 2bc.cosB
a² = 5² + 7² - 2 * 5 * 7 * cos60°
a² = 25 + 49 - 70 * (1/2)
a² = 34
a = √34 ≈ 5.83 cm

Kết luận

Định lý Cosin là một công cụ hữu ích để giải quyết các bài toán liên quan đến tam giác. Việc hiểu và áp dụng thành thạo định lý này sẽ giúp bạn giải quyết được nhiều bài toán phức tạp hơn.

Xem thêm: màu trắng tiếng anh gọi là gì

Sản phẩm liên quan: hồ công nghệ 4 lớp đáy là gì

Sản phẩm liên quan: bị vật nhọn chọc vào mắt

Sản phẩm hữu ích: đêm đom đóm và em

Xem thêm: giá thịt thỏ hơi hiện nay