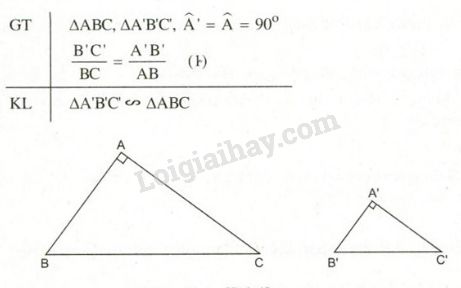
Điều Kiện Tạo Thành Tam Giác

Mô tả sản phẩm

Để tạo thành một tam giác, cần thỏa mãn điều kiện: tổng độ dài hai cạnh bất kỳ phải lớn hơn độ dài cạnh còn lại. Cụ thể hơn, nếu a, b, c là độ dài ba cạnh của một tam giác, thì ta phải có: a + b > c; a + c > b; và b + c > a. Nếu bất kỳ điều kiện nào trong ba điều kiện này không được thỏa mãn, thì ba đoạn thẳng đó không thể tạo thành một tam giác.

Các trường hợp đặc biệt

Tam giác đều:

Ba cạnh có độ dài bằng nhau (a = b = c).

Tam giác cân:

Hai cạnh có độ dài bằng nhau (a = b hoặc a = c hoặc b = c).

Tam giác vuông:

Thỏa mãn định lý Pytago: a² + b² = c² (với c là cạnh huyền). Điều kiện trên là điều kiện cần và đủ để tạo thành một tam giác trên mặt phẳng. Hiểu rõ điều kiện này giúp chúng ta xác định xem ba đoạn thẳng cho trước có thể tạo thành một tam giác hay không, và từ đó phân loại tam giác dựa trên độ dài các cạnh. Việc áp dụng điều kiện này rất quan trọng trong nhiều lĩnh vực, từ hình học cơ bản đến các ứng dụng phức tạp hơn trong toán học và kỹ thuật. Bằng cách kiểm tra ba bất đẳng thức trên, ta có thể nhanh chóng xác định khả năng tạo thành tam giác của ba đoạn thẳng cho trước. Hãy nhớ rằng, điều kiện này không chỉ áp dụng cho tam giác trên mặt phẳng mà còn có thể mở rộng sang các không gian đa chiều khác.

Sản phẩm liên quan: truyện con thỏ không ăn cỏ gần hang

Sản phẩm hữu ích: sờ chim nhiều có sao không

Sản phẩm liên quan: ngựa ngủ đứng hay nằm

Xem thêm: ngân hàng vietcombank làm việc tới mấy giờ

Xem thêm: điện trở dùng để làm gì