Điều kiện để phương trình có 2 nghiệm phân biệt

Mô tả sản phẩm

Điều kiện để phương trình bậc hai có hai nghiệm phân biệt là delta (biệt thức) phải lớn hơn 0.

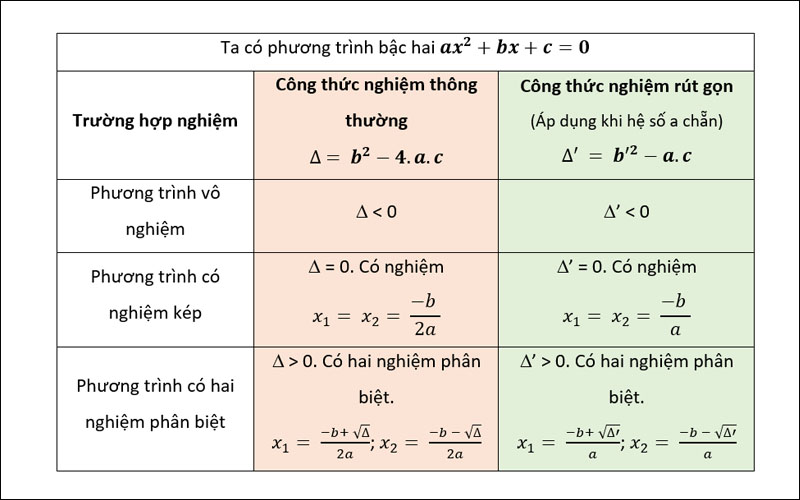
Phương trình bậc hai và biệt thức delta

Định nghĩa

Phương trình bậc hai tổng quát có dạng: ax² + bx + c = 0 (với a ≠ 0). Biệt thức delta (Δ) được tính theo công thức: Δ = b² - 4ac.

Điều kiện để phương trình có 2 nghiệm phân biệt

Để phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt, điều kiện cần và đủ là biệt thức delta (Δ) phải lớn hơn 0, tức là: Δ = b² - 4ac > 0. Khi đó, hai nghiệm phân biệt được tính theo công thức: x₁ = (-b + √Δ) / 2a và x₂ = (-b - √Δ) / 2a.

Ví dụ minh họa

Ví dụ 1:

Xét phương trình x² - 5x + 6 = 0. Ta có a = 1, b = -5, c = 6. Vậy Δ = (-5)² - 4(1)(6) = 25 - 24 = 1 > 0. Vì Δ > 0, phương trình có hai nghiệm phân biệt.

Ví dụ 2:

Xét phương trình x² + 4x + 4 = 0. Ta có a = 1, b = 4, c = 4. Vậy Δ = 4² - 4(1)(4) = 16 - 16 = 0. Vì Δ = 0, phương trình có nghiệm kép.

Ví dụ 3:

Xét phương trình x² + x + 1 = 0. Ta có a = 1, b = 1, c = 1. Vậy Δ = 1² - 4(1)(1) = 1 - 4 = -3 < 0. Vì Δ < 0, phương trình vô nghiệm.

Tổng kết

Điều kiện cần và đủ để phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) có hai nghiệm phân biệt là biệt thức delta (Δ) phải lớn hơn 0 (Δ = b² - 4ac > 0). Hiểu rõ điều kiện này giúp chúng ta giải quyết nhanh chóng và chính xác các bài toán liên quan đến nghiệm của phương trình bậc hai.

Sản phẩm liên quan: chiều dài rộng

Sản phẩm liên quan: hình ảnh búp bê

Sản phẩm hữu ích: lực ma sát trượt xuất hiện trong trường hợp nào

Sản phẩm liên quan: axit tác dụng với bazo tạo ra gì

Sản phẩm liên quan: thước đo chiều cao