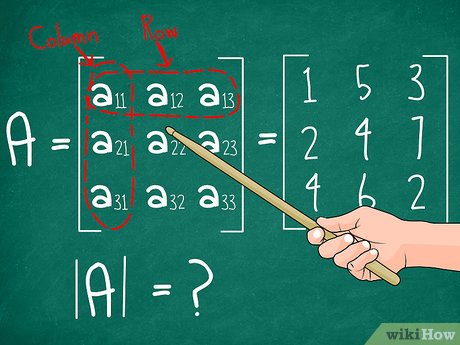
Det của ma trận là gì?

Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Định thức (det) của một ma trận vuông là một số được tính toán từ các phần tử của ma trận đó. Nó cung cấp thông tin quan trọng về ma trận, chẳng hạn như tính khả nghịch của ma trận. Nếu định thức của ma trận bằng 0, ma trận đó không khả nghịch (singular). Ngược lại, nếu định thức khác 0, ma trận đó khả nghịch.
Cách tính det của ma trận
Định thức của ma trận 2x2
Cho ma trận A = [[a, b], [c, d]], định thức của A (det(A)) được tính như sau: det(A) = ad - bc.Định thức của ma trận 3x3
Cho ma trận A = [[a, b, c], [d, e, f], [g, h, i]], định thức của A có thể được tính bằng quy tắc Sarrus hoặc bằng cách khai triển theo hàng hoặc cột. Quy tắc Sarrus đơn giản hơn với ma trận 3x3 nhưng không áp dụng được cho ma trận có cấp lớn hơn.Định thức của ma trận cấp cao hơn
Đối với ma trận có cấp lớn hơn 3, việc tính định thức trở nên phức tạp hơn. Các phương pháp phổ biến bao gồm khai triển Laplace (khai triển theo hàng hoặc cột) hoặc sử dụng các phép biến đổi hàng/cột để đưa ma trận về dạng tam giác trên hoặc tam giác dưới, sau đó tích các phần tử trên đường chéo chính. Các phần mềm toán học như MATLAB, Mathematica, hoặc các thư viện Python như NumPy cung cấp các hàm để tính toán định thức một cách hiệu quả.Ứng dụng của det của ma trận
Định thức của ma trận có nhiều ứng dụng quan trọng trong toán học và các lĩnh vực khác như: * **Giải hệ phương trình tuyến tính:** Định thức được sử dụng trong quy tắc Cramer để giải hệ phương trình tuyến tính. * **Tìm ma trận nghịch đảo:** Một ma trận chỉ khả nghịch nếu định thức của nó khác 0. Định thức được sử dụng trong công thức tính ma trận nghịch đảo. * **Tính diện tích và thể tích:** Định thức có thể được sử dụng để tính diện tích của một hình bình hành hoặc thể tích của một khối đa diện. * **Hình học giải tích:** Định thức được sử dụng trong các phép biến đổi hình học như phép quay, phép chiếu, v.v.Xem thêm: thanh xuan vat va
Xem thêm: gà ô chân xanh mắt ếch
Sản phẩm hữu ích: giới hạn đo là gì
Xem thêm: giáo án cá vàng bơi
Sản phẩm hữu ích: ca(hco3)2 có tan trong nước không