Understanding Derivatives in Calculus

Mô tả sản phẩm

A derivative in mathematics measures the instantaneous rate of change of a function. In simpler terms, it tells you how much a function's output changes for a tiny change in its input. This is crucial for understanding slopes of curves, optimization problems, and much more.

Key Concepts of Derivatives

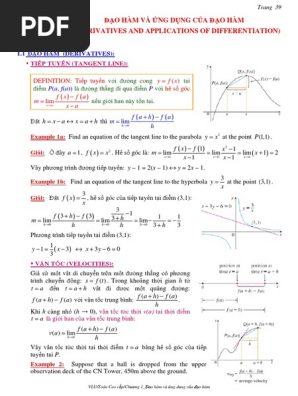
The Definition of a Derivative

The derivative of a function f(x) at a point x is defined as the limit of the difference quotient as the change in x approaches zero: f'(x) = lim (h→0) [(f(x + h) - f(x)) / h]. This limit represents the instantaneous slope of the tangent line to the function's graph at point x.

Interpreting the Derivative

The derivative, often denoted as f'(x) or df/dx, has several interpretations:

• Instantaneous Rate of Change: How quickly the function's value is changing at a specific point.
• Slope of the Tangent Line: The derivative gives the slope of the line that just touches the curve at a given point.
• Velocity and Acceleration: In physics, the derivative of position with respect to time is velocity, and the derivative of velocity with respect to time is acceleration.

Applications of Derivatives

Optimization Problems

Derivatives are essential for finding maximum and minimum values of functions. By setting the derivative equal to zero and solving, we can locate critical points, which are potential locations for maxima or minima.

Related Rates

Derivatives allow us to analyze how the rates of change of different variables are related. For instance, we can determine how fast the area of a circle is changing if its radius is changing at a known rate.

Curve Sketching

By examining the first and second derivatives of a function, we can determine its increasing/decreasing intervals, concavity, and inflection points, thus facilitating accurate curve sketching.

Practical Examples

Consider the function representing the position of a moving object. The derivative of this function gives its velocity, while the derivative of the velocity function provides its acceleration. In economics, derivatives can model marginal cost or revenue, providing insights for businesses. The applications of derivatives are far-reaching and extend to numerous fields.

Sản phẩm hữu ích: tiêu chuẩn làm thực tập sinh hybe

Sản phẩm liên quan: bài tập tìm x lớp 2

Xem thêm: 6 múi tiếng anh là gì

Sản phẩm liên quan: kí hiệu hạt nhân nguyên tử

Sản phẩm liên quan: 550ml bằng bao nhiêu lít