Đạo Hàm Mở Rộng: Khái Niệm, Ứng Dụng và Ví Dụ Minh Họa


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
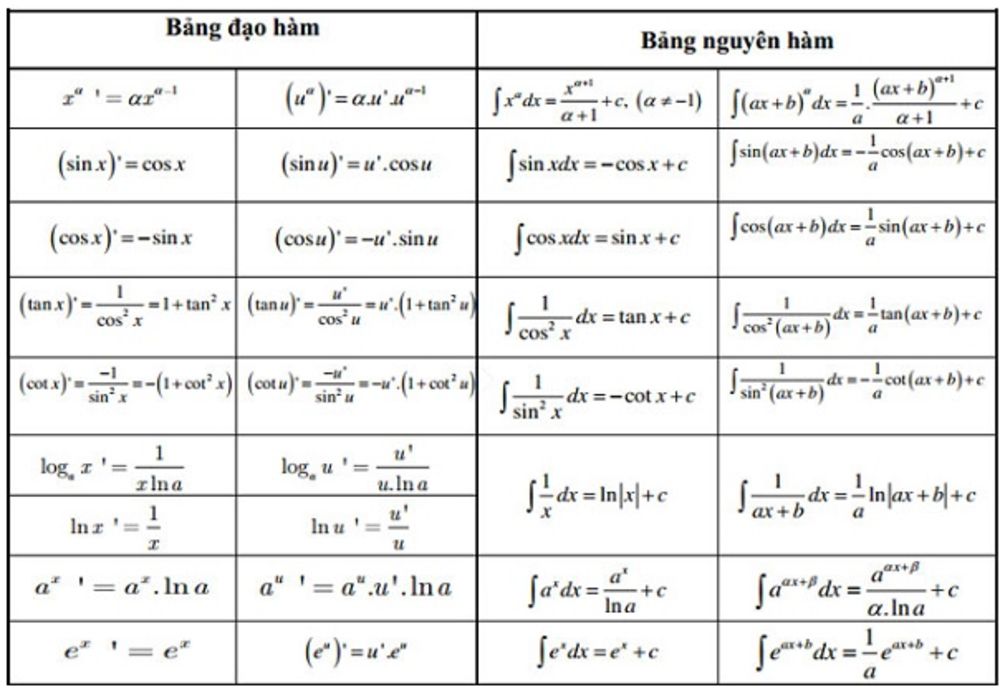
Đạo hàm mở rộng, hay còn gọi là đạo hàm cấp cao hơn, là khái niệm mở rộng từ đạo hàm bậc nhất, cho phép ta tính toán tốc độ thay đổi của chính đạo hàm. Nói một cách đơn giản, đạo hàm bậc hai cho biết tốc độ thay đổi của tốc độ thay đổi, đạo hàm bậc ba cho biết tốc độ thay đổi của gia tốc, và cứ thế tiếp tục. Việc hiểu đạo hàm mở rộng rất quan trọng trong nhiều lĩnh vực như vật lý, kỹ thuật, kinh tế...
Khái niệm đạo hàm mở rộng
Đạo hàm cấp n
Đạo hàm cấp n của một hàm số f(x), ký hiệu là f(n)(x), được định nghĩa là đạo hàm của đạo hàm cấp (n-1). Ví dụ: đạo hàm bậc hai là đạo hàm của đạo hàm bậc nhất, đạo hàm bậc ba là đạo hàm của đạo hàm bậc hai, v.v... Tồn tại một số hàm số không có đạo hàm cấp n với n đủ lớn, tức là đạo hàm của chúng không xác định được sau một số bậc nhất định. Công thức tính toán đạo hàm cấp n phụ thuộc vào hàm số cụ thể và thường đòi hỏi kỹ thuật tính toán phức tạp hơn đạo hàm bậc nhất.
Ứng dụng của đạo hàm mở rộng
Đạo hàm mở rộng có ứng dụng rộng rãi trong nhiều lĩnh vực:
- Vật lý: Tính toán gia tốc, lực, mômen, ...
- Kỹ thuật: Phân tích tín hiệu, tối ưu hóa thiết kế, điều khiển tự động,
- Kinh tế: Phân tích độ lồi lõm của hàm lợi nhuận, điểm cực đại cực tiểu.
- Toán học: Xác định cực trị của hàm số, nghiên cứu tính chất của hàm số.
Ví dụ minh họa
Ví dụ về đạo hàm bậc hai
Cho hàm số f(x) = x3 - 6x2 + 9x + 2. Đạo hàm bậc nhất là f'(x) = 3x2 - 12x + 9. Đạo hàm bậc hai là f''(x) = 6x - 12. Đạo hàm bậc hai này cho biết tốc độ thay đổi của tốc độ thay đổi của hàm số f(x).
Ứng dụng thực tiễn
Ví dụ, trong vật lý, nếu f(x) biểu diễn vị trí của một vật thể theo thời gian, thì đạo hàm bậc nhất f'(x) là vận tốc và đạo hàm bậc hai f''(x) là gia tốc. Hiểu được gia tốc giúp ta dự đoán chuyển động của vật thể một cách chính xác hơn.
Tóm lại, đạo hàm mở rộng là một công cụ mạnh mẽ trong toán học và các ứng dụng thực tiễn. Việc hiểu rõ khái niệm và ứng dụng của nó là rất quan trọng cho việc giải quyết nhiều bài toán phức tạp.
Sản phẩm liên quan: tô màu hươu cao cổ
Sản phẩm liên quan: 1 sào ruộng bao nhiêu tiền
Sản phẩm hữu ích: vinschool tuyển dụng giáo viên tiếng anh
Sản phẩm liên quan: lời bài hát lệ úa