Đạo Hàm Logarit Công Thức

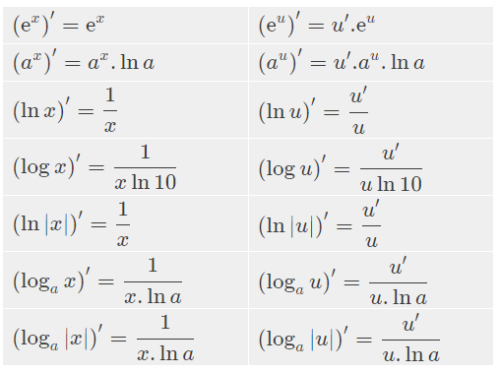
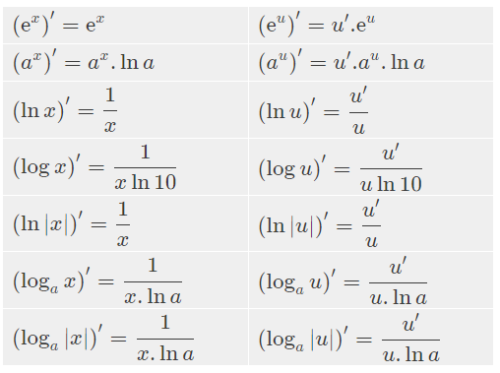
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Đạo hàm của hàm logarit là một công cụ quan trọng trong giải tích. Bài viết này sẽ cung cấp cho bạn công thức đạo hàm logarit cơ bản và mở rộng, giúp bạn hiểu rõ và áp dụng vào các bài toán. Công thức đạo hàm logarit cơ bản là: d/dx (ln|x|) = 1/x. Tuy nhiên, tùy thuộc vào cơ số và biến số, công thức sẽ có những biến thể.
Công thức đạo hàm logarit cơ bản
Đạo hàm logarit tự nhiên (ln x)
Đạo hàm của hàm logarit tự nhiên (cơ số e) là:
d/dx (ln|x|) = 1/x (với x ≠ 0)
Lưu ý: Giá trị tuyệt đối |x| được sử dụng để đảm bảo miền xác định của hàm logarit tự nhiên.
Đạo hàm logarit cơ số a (logax)
Đạo hàm của hàm logarit cơ số a (a > 0, a ≠ 1) là:
d/dx (logax) = 1/(x ln a) (với x > 0)
Công thức này được suy ra từ công thức đổi cơ số logarit và đạo hàm logarit tự nhiên.
Công thức đạo hàm logarit mở rộng
Đạo hàm của hàm hợp chứa logarit
Nếu có hàm hợp dạng y = ln[f(x)], đạo hàm của nó được tính theo quy tắc dây chuyền:
dy/dx = [f'(x)] / f(x)
Ví dụ: Nếu y = ln(x² + 1), thì dy/dx = (2x) / (x² + 1)
Đạo hàm của hàm logarit với cơ số và biến số phức tạp hơn
Đối với các hàm logarit phức tạp hơn, ta cần sử dụng các quy tắc đạo hàm khác nhau như quy tắc tích, quy tắc thương, quy tắc dây chuyền kết hợp với các công thức đạo hàm logarit cơ bản đã nêu ở trên. Việc lựa chọn quy tắc đạo hàm phù hợp phụ thuộc vào cấu trúc của hàm số.
Hiểu rõ các công thức đạo hàm logarit sẽ giúp bạn giải quyết nhiều bài toán trong giải tích, đặc biệt trong các lĩnh vực như vật lý, kinh tế và kỹ thuật.
Xem thêm: trò chơi luyện chuột lớp 3
Xem thêm: tam giác anh phan
Sản phẩm hữu ích: nước là dung môi gì
Xem thêm: lời bài hát đêm huyền diệu
Sản phẩm hữu ích: nằm mơ lượm được vàng