Đạo Hàm Là Gì?


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Đạo hàm của một hàm số tại một điểm thể hiện tốc độ thay đổi tức thời của hàm số tại điểm đó. Nói một cách đơn giản, nó cho biết hàm số đang tăng hay giảm và mức độ nhanh chậm của sự thay đổi đó.
Khái niệm cơ bản về đạo hàm
Định nghĩa toán học
Đạo hàm của hàm số f(x) tại điểm x0, ký hiệu là f'(x0) hoặc df(x)/dx|x=x0, được định nghĩa là giới hạn (nếu tồn tại): f'(x0) = lim(x→x0) [f(x) - f(x0)] / (x - x0) Điều này có nghĩa là đạo hàm là tỷ lệ thay đổi của hàm số khi biến x tiến tới x0. Nếu giới hạn này tồn tại, ta nói hàm số f(x) khả vi tại x0.Ý nghĩa hình học
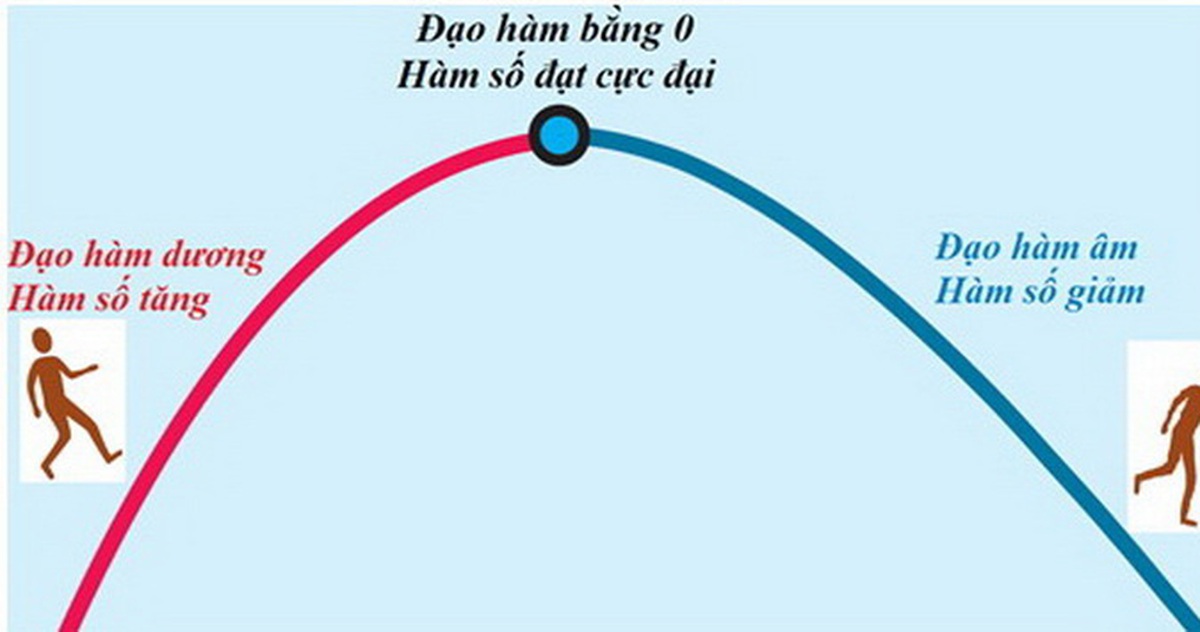
Về mặt hình học, đạo hàm tại một điểm trên đồ thị của hàm số chính là hệ số góc của tiếp tuyến với đồ thị tại điểm đó. Hệ số góc này cho biết độ dốc của tiếp tuyến, từ đó phản ánh tốc độ thay đổi của hàm số tại điểm đó. Nếu đạo hàm dương, hàm số tăng; nếu đạo hàm âm, hàm số giảm; nếu đạo hàm bằng 0, hàm số có thể đạt cực trị (cực đại hoặc cực tiểu).Ứng dụng của đạo hàm
Đạo hàm có ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:Toán học
* Tìm cực trị của hàm số. * Xác định tính đơn điệu của hàm số. * Tính tích phân. * Giải phương trình vi phân.Vật lý
* Tính vận tốc và gia tốc của một vật thể chuyển động. * Xác định lực và mô men. * Mô tả các hiện tượng biến đổi liên tục.Kinh tế
* Phân tích tối ưu hóa lợi nhuận. * Nghiên cứu sự biến đổi của chi phí và doanh thu. * Xây dựng các mô hình kinh tế động.Sản phẩm liên quan: chị ơi nước miếng
Sản phẩm hữu ích: diện tích xung quanh hình hộp chữ nhật là gì
Sản phẩm hữu ích: xê hát là chữ gì lớp 3
Xem thêm: vôi nước quét tường
Sản phẩm hữu ích: từ phổ la gì lớp 7