Công thức hạ bậc lượng giác
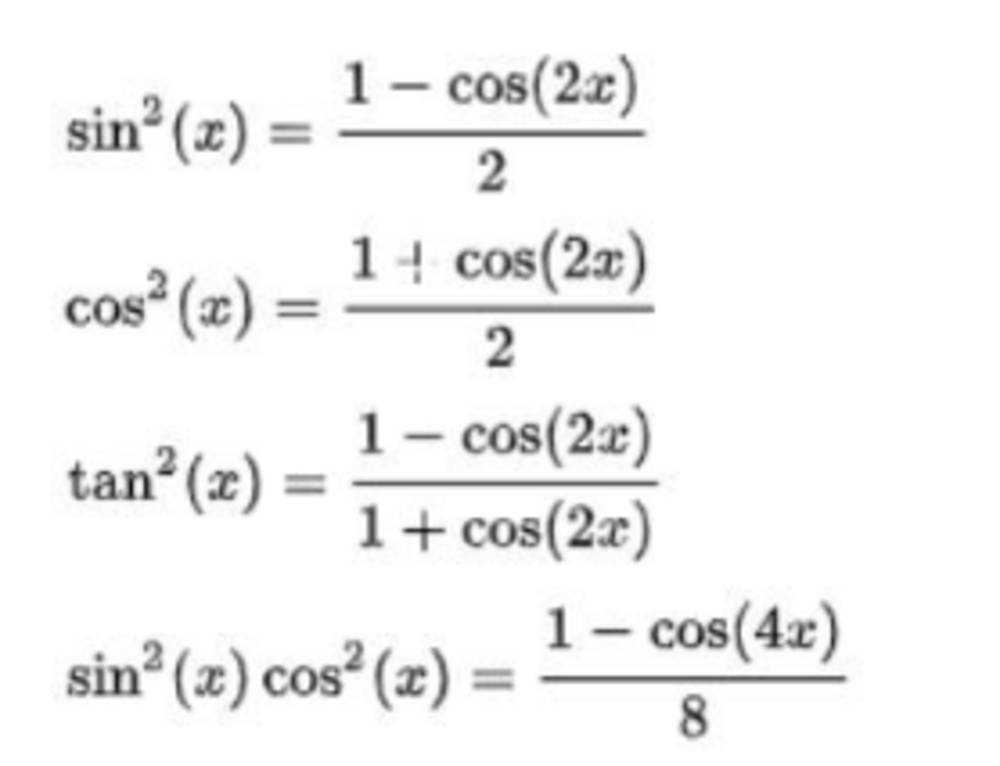

Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Công thức hạ bậc lượng giác dùng để biến đổi các biểu thức lượng giác có bậc cao (như bình phương, lập phương...) thành các biểu thức có bậc thấp hơn, thường là bậc nhất. Việc sử dụng công thức hạ bậc giúp đơn giản hóa các biểu thức, từ đó dễ dàng tính toán và giải quyết các bài toán lượng giác phức tạp hơn.
Các công thức hạ bậc lượng giác cơ bản
Công thức hạ bậc bình phương
- cos2x = (1 + cos2x)/2
- sin2x = (1 - cos2x)/2
Công thức hạ bậc tích sin và cos
- sin x cos x = (1/2)sin2x
Từ các công thức cơ bản trên, ta có thể suy ra các công thức hạ bậc khác phức tạp hơn. Ví dụ, để hạ bậc sin3x, ta có thể viết sin3x = sin x . sin2x = sin x (1 - cos2x) rồi tiếp tục sử dụng công thức hạ bậc cho cos2x. Việc vận dụng linh hoạt các công thức này giúp giải quyết nhiều bài toán lượng giác một cách hiệu quả.
Ứng dụng của công thức hạ bậc lượng giác
Công thức hạ bậc lượng giác được ứng dụng rộng rãi trong nhiều lĩnh vực, đặc biệt là:
- Giải phương trình lượng giác: Hạ bậc giúp đưa phương trình về dạng đơn giản hơn, dễ dàng tìm nghiệm.
- Tính tích phân lượng giác: Việc hạ bậc giúp đơn giản hóa tích phân, làm cho việc tính toán dễ dàng hơn.
- Ứng dụng trong vật lý: Trong nhiều bài toán vật lý, đặc biệt là các bài toán liên quan đến dao động điều hòa, sóng, công thức hạ bậc lượng giác đóng vai trò quan trọng.
Để thành thạo việc sử dụng công thức hạ bậc lượng giác, cần luyện tập nhiều bài tập khác nhau. Bằng cách đó, bạn sẽ nắm vững các công thức và biết cách áp dụng chúng vào các bài toán một cách linh hoạt và hiệu quả.
Xem thêm: máy đào gầu thuận
Sản phẩm liên quan: xs nhỏ hơn s
Xem thêm: vẽ trang trí cái đĩa