Nguyên hàm của cos2x
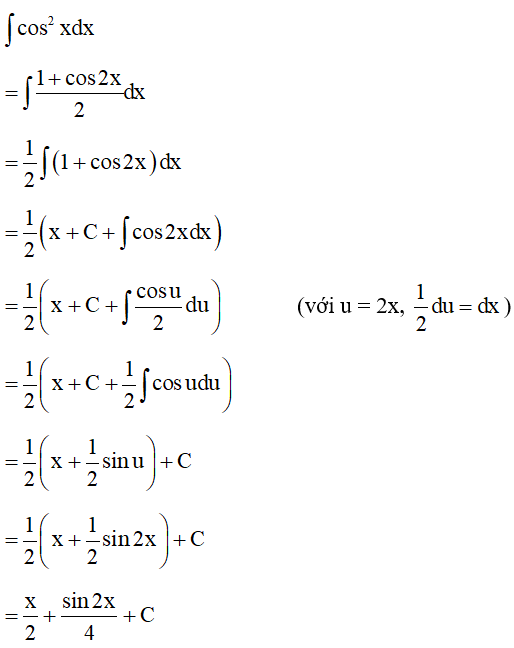
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Nguyên hàm của cos2x là (1/2)sin2x + C, trong đó C là hằng số tích phân.
Công thức nguyên hàm của cos2x
Bắt đầu từ nguyên hàm cơ bản
Để tìm nguyên hàm của cos2x, ta cần nhớ lại nguyên hàm cơ bản của hàm cos(u): ∫cos(u)du = sin(u) + C. Trong trường hợp này, u = 2x. Do đó, ta cần sử dụng phương pháp đổi biến để tính nguyên hàm.
Áp dụng phương pháp đổi biến
Đặt u = 2x, suy ra du = 2dx, hoặc dx = du/2. Thay vào nguyên hàm, ta có:
∫cos(2x)dx = ∫cos(u) (du/2) = (1/2)∫cos(u)du = (1/2)sin(u) + C
Thay u = 2x trở lại, ta được kết quả cuối cùng:
∫cos(2x)dx = (1/2)sin(2x) + C
Ví dụ minh họa
Tính nguyên hàm của cos(2x) từ 0 đến π/4
Ta có nguyên hàm của cos(2x) là (1/2)sin(2x) + C. Để tính tích phân xác định từ 0 đến π/4, ta thực hiện như sau:
(1/2)sin(2(π/4)) - (1/2)sin(2(0)) = (1/2)sin(π/2) - (1/2)sin(0) = (1/2)(1) - (1/2)(0) = 1/2
Vậy tích phân xác định của cos(2x) từ 0 đến π/4 là 1/2.
Kết luận
Như vậy, nguyên hàm của cos2x là một khái niệm quan trọng trong giải tích. Hiểu rõ công thức và cách áp dụng sẽ giúp bạn giải quyết nhiều bài toán liên quan đến tích phân và đạo hàm một cách hiệu quả.
Sản phẩm hữu ích: phát biểu nào sau đây không đúng với dân cư hoa kỳ
Sản phẩm hữu ích: cuộc cải cách của lê thánh tông
Sản phẩm hữu ích: trung điểm của tam giác cân
Xem thêm: các chức năng cơ bản của thị trường
Sản phẩm liên quan: lời bài hát tình em tháp mười