Công thức tổng quát của nhị thức Newton
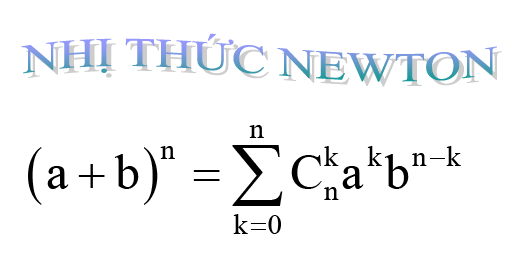
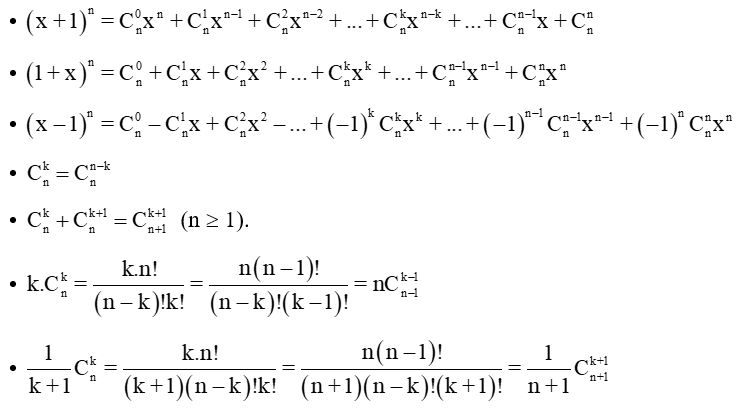
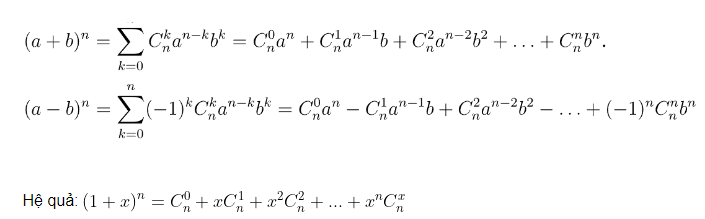
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Công thức tổng quát của nhị thức Newton cho phép ta khai triển một lũy thừa của tổng hai số hạng thành một đa thức. Cụ thể, công thức này mô tả cách viết (a + b)n dưới dạng một tổng các số hạng, mỗi số hạng chứa các hệ số nhị thức và các lũy thừa của a và b.
Công thức tổng quát
Định nghĩa
Công thức tổng quát của nhị thức Newton là: (a + b)n = Σnk=0 (n k) an-k bk, trong đó: * n là một số nguyên không âm. * k là chỉ số chạy từ 0 đến n. * (n k) là tổ hợp chập k của n phần tử, được tính bằng công thức: (n k) = n! / (k! (n-k)!), với n! là giai thừa của n (n! = n × (n-1) × (n-2) × ... × 2 × 1). * a và b là hai số hạng bất kỳ.Giải thích các thành phần
* (n k): Đây là hệ số nhị thức, biểu thị số cách chọn k phần tử từ một tập hợp có n phần tử. Chúng còn được gọi là hệ số tổ hợp. * an-k: Lũy thừa của số hạng đầu tiên a, với số mũ giảm dần từ n xuống 0. * bk: Lũy thừa của số hạng thứ hai b, với số mũ tăng dần từ 0 lên n. * Σnk=0: Ký hiệu này chỉ tổng của tất cả các số hạng từ k = 0 đến k = n.Ví dụ minh họa
Hãy áp dụng công thức để khai triển (x + y)3: (x + y)3 = Σ3k=0 (3 k) x3-k yk = (3 0)x3y0 + (3 1)x2y1 + (3 2)x1y2 + (3 3)x0y3 = x3 + 3x2y + 3xy2 + y3Ứng dụng của công thức nhị thức Newton
Công thức nhị thức Newton có ứng dụng rộng rãi trong nhiều lĩnh vực toán học và khoa học, bao gồm: * Tính toán xác suất. * Giải tích. * Đại số tuyến tính. * Lý thuyết đồ thị.Xem thêm: lời bài hát đi đu đưa đi
Sản phẩm liên quan: kháng sinh chấm mụn
Xem thêm: nhiệt lượng kí hiệu là gì