Công thức tính thể tích tứ diện
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Công thức tính thể tích tứ diện là V = 1/6|a.(b x c)|, trong đó a, b, c là ba vectơ cạnh của tứ diện. Đây là công thức tổng quát và được sử dụng rộng rãi. Bài viết dưới đây sẽ giải thích chi tiết hơn về công thức này và các trường hợp cụ thể.
Các cách tính thể tích tứ diện
Công thức tính thể tích tứ diện dựa trên tích hỗn tạp
Công thức tính thể tích tứ diện dựa trên tích hỗn tạp của ba vectơ tạo thành ba cạnh xuất phát từ cùng một đỉnh là cách tính phổ biến nhất. Giả sử tứ diện ABCD có các đỉnh A, B, C, D. Ta chọn một đỉnh, ví dụ đỉnh A, và xét ba vectơ AB, AC, AD. Thể tích V của tứ diện được tính bởi công thức:V = 1/6 |AB . (AC x AD)|
Trong đó:
- AB, AC, AD là các vectơ.
- "." là tích vô hướng.
- "x" là tích có hướng.
- || biểu thị giá trị tuyệt đối.
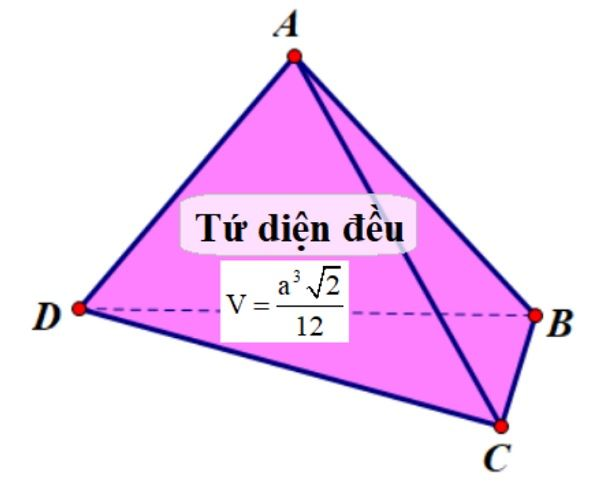
Công thức tính thể tích tứ diện đều
Đối với trường hợp đặc biệt là tứ diện đều, với cạnh a, công thức tính thể tích đơn giản hơn:V = a³ / 6√2
Công thức này được suy ra từ công thức tổng quát, nhưng đã được đơn giản hóa cho trường hợp tứ diện đều.
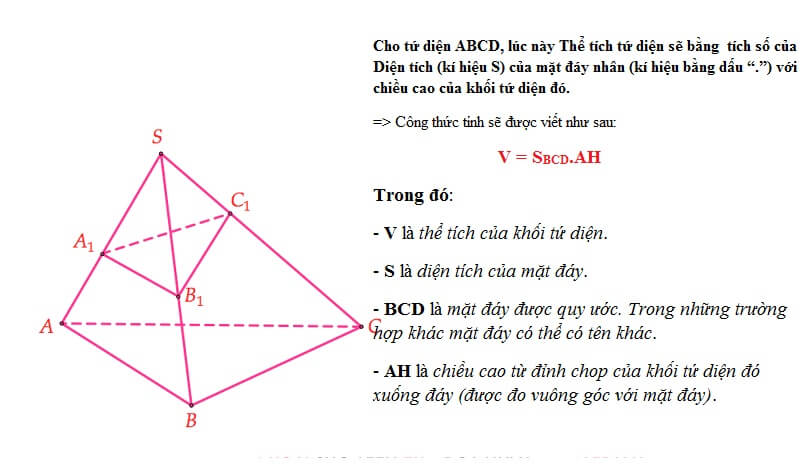
Công thức tính thể tích tứ diện khi biết diện tích đáy và chiều cao
Tương tự như hình chóp, thể tích tứ diện cũng có thể tính bằng công thức:V = 1/3 * S * h
Trong đó:
- S là diện tích của một mặt của tứ diện (được coi là đáy).
- h là chiều cao tương ứng với mặt đáy đó.
Việc lựa chọn công thức nào phụ thuộc vào dữ liệu đã biết. Nếu biết tọa độ các đỉnh, công thức tích hỗn tạp là lựa chọn tốt nhất. Nếu là tứ diện đều, công thức rút gọn sẽ đơn giản hơn nhiều. Hiểu rõ các công thức và cách áp dụng sẽ giúp bạn giải quyết các bài toán liên quan đến thể tích tứ diện một cách chính xác và hiệu quả.
Xem thêm: cách tính điểm trung bình các môn
Xem thêm: nêu ý nghĩa của điện trở suất
Sản phẩm liên quan: công thức tính trọng lượng riêng của chất lỏng