Công thức tính định thức

Mô tả sản phẩm

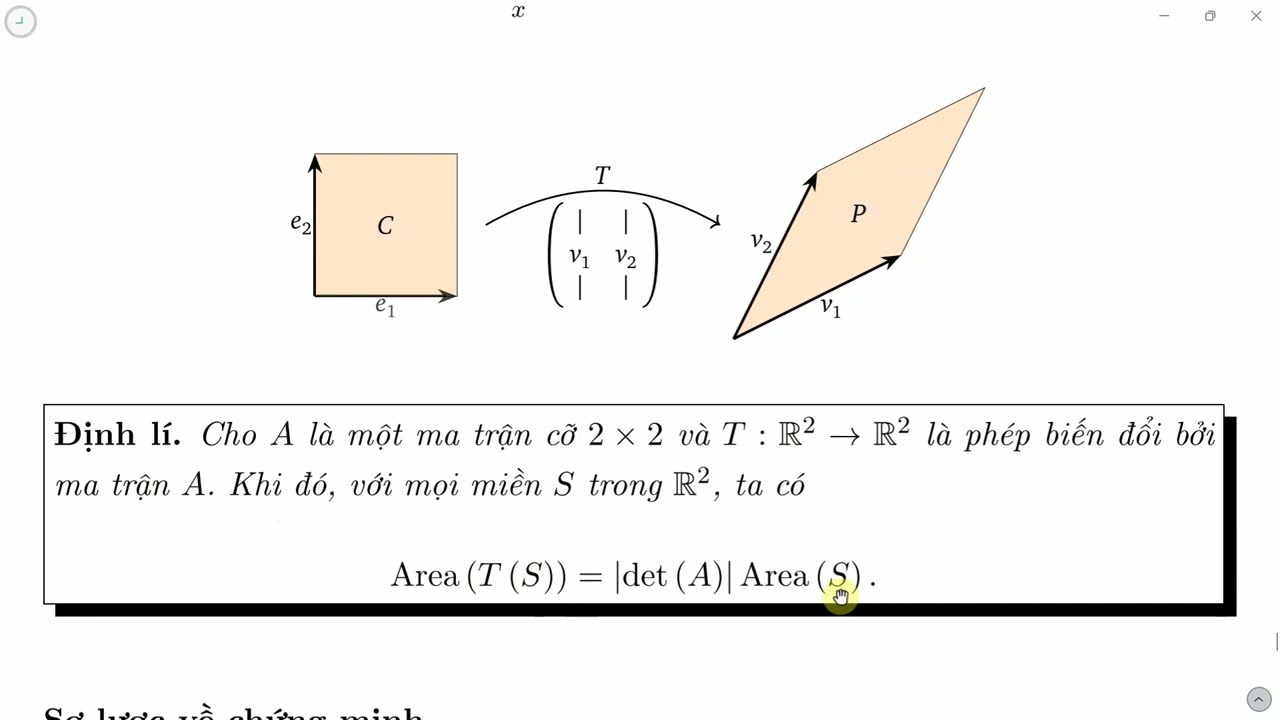
Công thức tính định thức phụ thuộc vào cấp của ma trận. Đối với ma trận 2x2, định thức được tính bằng tích các phần tử trên đường chéo chính trừ đi tích các phần tử trên đường chéo phụ. Đối với ma trận cấp cao hơn, ta sử dụng phương pháp khai triển Laplace hoặc quy tắc Sarrus (đối với ma trận 3x3).

Công thức tính định thức ma trận 2x2

Công thức:

Cho ma trận A = [[a, b], [c, d]], định thức của A (ký hiệu là det(A) hoặc |A|) được tính bằng:

|A| = ad - bc

Công thức tính định thức ma trận 3x3

Quy tắc Sarrus:

Đối với ma trận 3x3, ta có thể sử dụng quy tắc Sarrus để tính định thức. Viết lại hai cột đầu tiên của ma trận bên phải ma trận ban đầu. Định thức được tính bằng tổng của tích các phần tử trên ba đường chéo chính hướng xuống trừ đi tổng của tích các phần tử trên ba đường chéo chính hướng lên.

Cho ma trận A = [[a, b, c], [d, e, f], [g, h, i]], định thức của A được tính bằng:

|A| = aei + bfg + cdh - ceg - bdi - afh

Công thức tính định thức ma trận cấp n

Khai triển Laplace:

Đối với ma trận cấp n (n ≥ 2), phương pháp phổ biến nhất để tính định thức là khai triển Laplace theo một hàng hoặc một cột. Khai triển Laplace theo hàng i được tính như sau:

|A| = Σ_j=1ⁿ (-1)^i+j * a_ij * |M_ij|

Trong đó:

• a_ij là phần tử ở hàng i, cột j của ma trận A.
• M_ij là ma trận con được tạo bằng cách loại bỏ hàng i và cột j của ma trận A.
• |M_ij| là định thức của ma trận con M_ij.

Quá trình này được lặp lại cho đến khi ta chỉ còn lại các ma trận 2x2 hoặc 1x1, lúc đó ta có thể tính định thức trực tiếp.

Việc lựa chọn hàng hoặc cột để khai triển Laplace có thể ảnh hưởng đến độ phức tạp của tính toán. Thông thường, nên chọn hàng hoặc cột có nhiều số 0 để giảm số lượng phép tính.

Xem thêm: kí tự trái tim rỗng

Sản phẩm hữu ích: màu xám tiếng anh đọc là gì

Sản phẩm liên quan: các số trong phép cộng gọi là gì

Xem thêm: hóa trị của p

Sản phẩm liên quan: bút vẽ lên vải