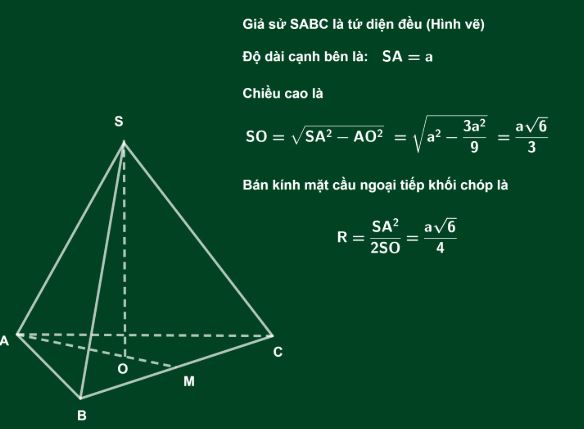
Công thức tính bán kính đường tròn ngoại tiếp tam giác

Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Công thức tính bán kính đường tròn ngoại tiếp tam giác là R = abc/(4S), trong đó a, b, c là độ dài ba cạnh tam giác và S là diện tích tam giác.
Các công thức tính bán kính đường tròn ngoại tiếp tam giác
Công thức dựa trên độ dài các cạnh và diện tích
Công thức phổ biến nhất để tính bán kính đường tròn ngoại tiếp tam giác là: R = abc/(4S), với:
- R: Bán kính đường tròn ngoại tiếp
- a, b, c: Độ dài ba cạnh của tam giác
- S: Diện tích của tam giác
Diện tích S có thể tính bằng công thức Heron: S = √(p(p-a)(p-b)(p-c)), với p là nửa chu vi tam giác (p = (a+b+c)/2).
Công thức dựa trên độ dài cạnh và góc
Bán kính đường tròn ngoại tiếp cũng có thể tính được dựa trên độ dài một cạnh và góc đối diện với cạnh đó:
R = a / (2sinA) = b / (2sinB) = c / (2sinC)
- a, b, c: Độ dài ba cạnh của tam giác
- A, B, C: Góc đối diện với các cạnh a, b, c tương ứng
Ví dụ minh họa
Giả sử ta có một tam giác với các cạnh a = 5, b = 6, c = 7. Diện tích tam giác tính được bằng công thức Heron là:
p = (5+6+7)/2 = 9
S = √(9(9-5)(9-6)(9-7)) = √(9*4*3*2) = √216 ≈ 14.7
Vậy bán kính đường tròn ngoại tiếp tam giác là:
R = (5*6*7) / (4*14.7) ≈ 3.56
Ứng dụng của công thức
Công thức tính bán kính đường tròn ngoại tiếp tam giác được ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
- Hình học: Xác định vị trí tâm đường tròn ngoại tiếp, giải các bài toán liên quan đến đường tròn.
- Kiến trúc: Thiết kế các công trình hình học.
- Trắc địa: Xác định vị trí các điểm trên mặt đất.
Sản phẩm liên quan: quá trình trao đổi khí ở người diễn ra theo cơ chế nào
Xem thêm: tranh vẽ cây tre
Sản phẩm liên quan: kieemr tra phat nguoi