Công thức Parabol Lớp 10
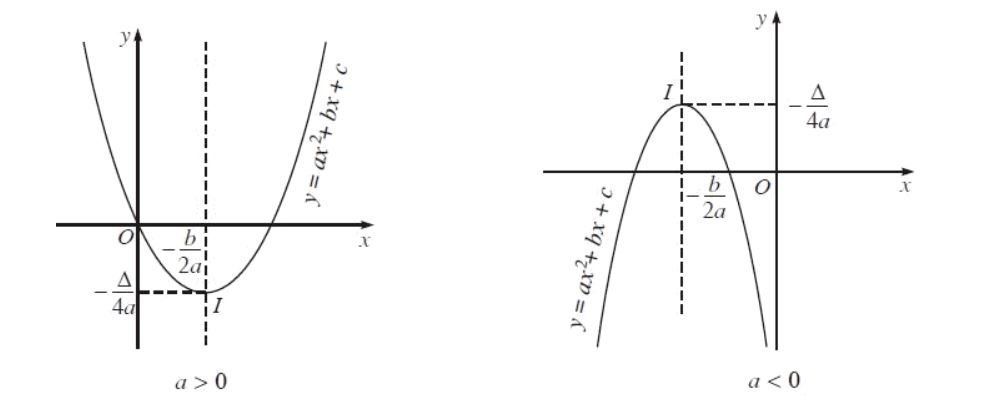

Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Công thức parabol lớp 10 thường được biểu diễn dưới dạng phương trình bậc hai y = ax² + bx + c (với a ≠ 0). Bài viết này sẽ giúp bạn hiểu rõ hơn về các dạng công thức và cách áp dụng chúng.
Dạng tổng quát của Parabol
Phương trình chính tắc:
Phương trình tổng quát của parabol là y = ax² + bx + c, trong đó a, b, c là các hệ số thực và a ≠ 0. Hệ số a quyết định chiều hướng mở của parabol (a > 0 thì parabol hướng lên, a < 0 thì parabol hướng xuống). Hệ số b và c ảnh hưởng đến vị trí của đỉnh parabol và giao điểm với trục Oy.
Tọa độ đỉnh Parabol:
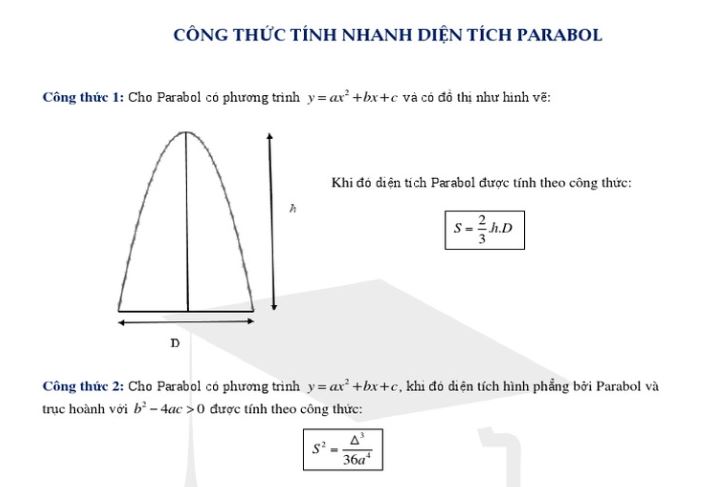
Đỉnh parabol có tọa độ là: xđỉnh = -b/(2a) và yđỉnh = -Δ/(4a), với Δ = b² - 4ac (biệt thức delta).
Trục đối xứng:
Trục đối xứng của parabol là đường thẳng x = -b/(2a), đi qua đỉnh parabol.
Các dạng toán thường gặp
Xác định phương trình parabol:
Để xác định phương trình parabol, ta cần tìm các hệ số a, b, c. Thông thường, ta sẽ được cung cấp các điểm thuộc parabol hoặc các thông tin về đỉnh, trục đối xứng. Từ đó, lập hệ phương trình và giải để tìm a, b, c.
Tìm giao điểm với trục Ox và Oy:
Giao điểm với trục Oy (trục tung) có tọa độ (0; c). Giao điểm với trục Ox (trục hoành) được tìm bằng cách giải phương trình ax² + bx + c = 0. Số nghiệm của phương trình này chính là số giao điểm của parabol với trục Ox.
Ứng dụng của Parabol:
Parabol có nhiều ứng dụng trong thực tế, ví dụ như trong việc thiết kế cầu, ăng-ten vệ tinh, đèn pha,… Hiểu rõ về công thức parabol giúp chúng ta giải quyết nhiều bài toán liên quan đến chuyển động ném xiên, quỹ đạo của vật thể.
Sản phẩm liên quan: khi nào xuất hiện dòng điện cảm ứng
Xem thêm: tính độ dịch chuyển
Sản phẩm liên quan: ong xây tổ lớp 3
Sản phẩm hữu ích: cách chơi cá ngựa
Sản phẩm hữu ích: tập gõ bàn phím