Công thức nội suy là gì?
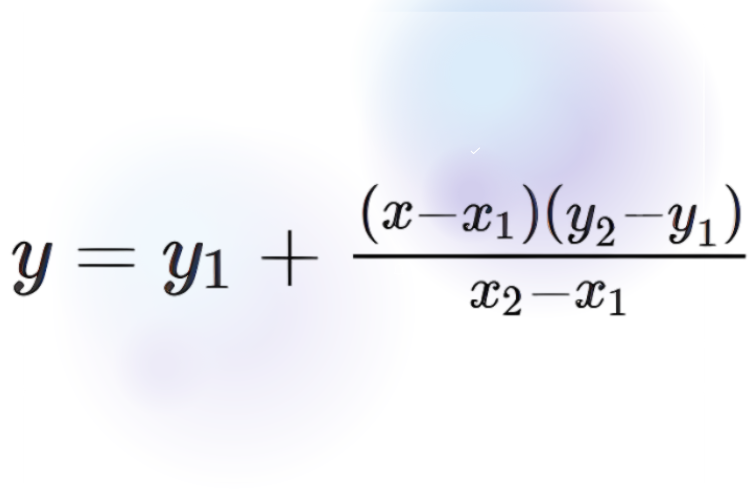

Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Công thức nội suy dùng để tìm giá trị của một hàm số tại một điểm nằm giữa các điểm đã biết. Tùy thuộc vào dữ liệu và yêu cầu tính toán, ta có thể sử dụng nhiều phương pháp nội suy khác nhau, chẳng hạn như nội suy tuyến tính, nội suy Lagrange, nội suy Newton, v.v... Mỗi phương pháp sẽ có công thức riêng.
Nội suy tuyến tính
Công thức
Nội suy tuyến tính là phương pháp đơn giản nhất, sử dụng để ước tính giá trị của hàm số tại một điểm nằm giữa hai điểm dữ liệu đã biết. Công thức nội suy tuyến tính được cho bởi:
y = y1 + (x - x1) * (y2 - y1) / (x2 - x1)
Trong đó:
x là giá trị cần tìm.
y là giá trị nội suy tương ứng.
(x1, y1) và (x2, y2) là hai điểm dữ liệu đã biết, sao cho x1 ≤ x ≤ x2.
Nội suy Lagrange
Công thức
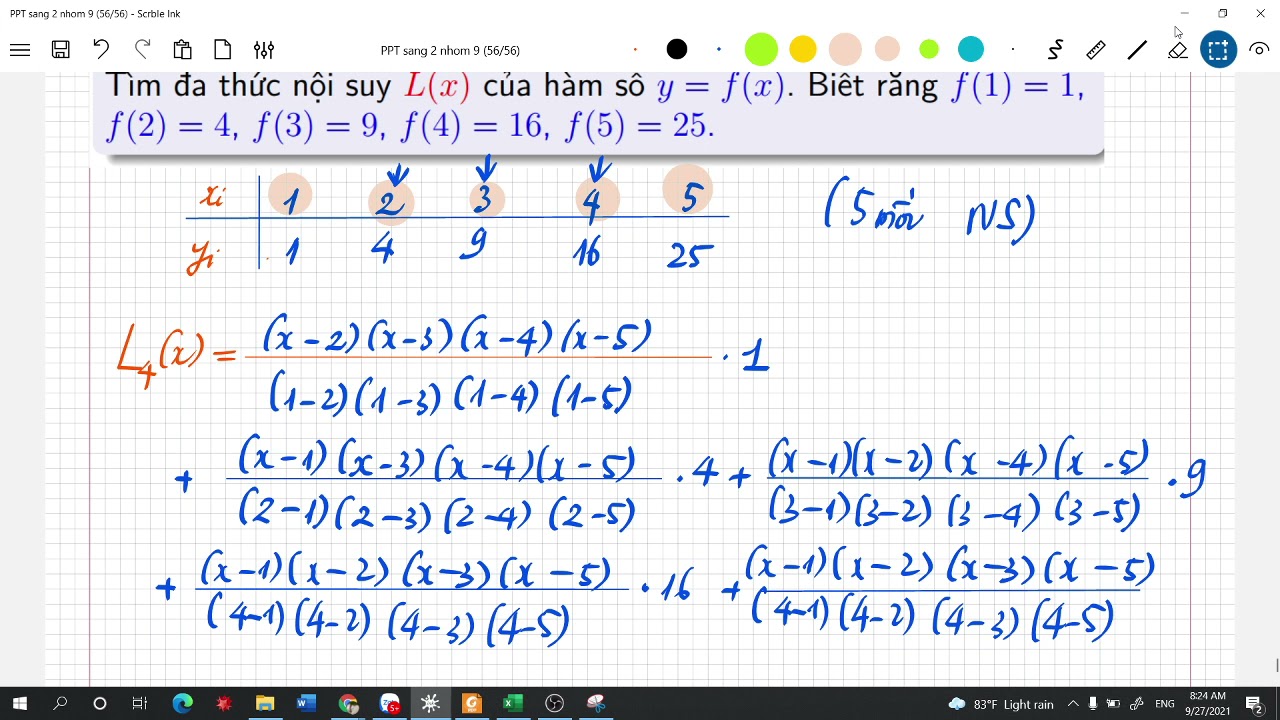
Nội suy Lagrange cho phép tìm một đa thức bậc n đi qua n+1 điểm dữ liệu đã biết. Công thức nội suy Lagrange cho một đa thức bậc n là:
Pn(x) = Σi=0n yi Li(x)
Trong đó:
Pn(x) là đa thức nội suy.
yi là giá trị của hàm số tại điểm xi.
Li(x) là đa thức cơ sở Lagrange, được định nghĩa như sau:
Li(x) = Πj=0, j≠in (x - xj) / (xi - xj)
Nội suy Newton
Công thức
Nội suy Newton sử dụng hiệu số chia để xây dựng đa thức nội suy. Công thức tổng quát phức tạp hơn, nhưng cơ bản dựa trên việc tính toán hiệu số chia và xây dựng đa thức dựa trên chúng. Ưu điểm của nội suy Newton là dễ dàng thêm điểm dữ liệu mới mà không cần tính toán lại toàn bộ đa thức.
Việc lựa chọn phương pháp nội suy phụ thuộc vào độ chính xác mong muốn, số lượng điểm dữ liệu và tính chất của hàm số. Nội suy tuyến tính đơn giản nhưng ít chính xác, trong khi nội suy Lagrange và Newton cung cấp độ chính xác cao hơn nhưng phức tạp hơn về mặt tính toán.
Sản phẩm liên quan: cuo h2o
Sản phẩm liên quan: hổ đi kiếm ăn giờ nào
Sản phẩm liên quan: soạn lịch sử 8 chân trời sáng tạo
Xem thêm: định nghĩa tiếng anh