Công thức logarit đạo hàm

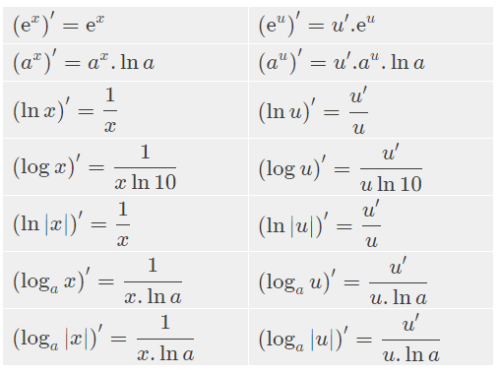
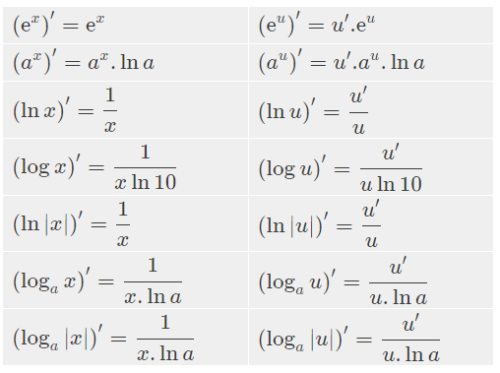
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Công thức đạo hàm của hàm logarit được sử dụng rộng rãi trong giải tích và các ứng dụng của nó. Bạn cần tìm hiểu cách tính đạo hàm của hàm logarit cơ số tự nhiên (ln x) và logarit cơ số a (logax)? Bài viết này sẽ cung cấp cho bạn đầy đủ công thức và ví dụ minh họa.
Đạo hàm của hàm logarit cơ số tự nhiên (ln x)
Công thức:
Đạo hàm của hàm logarit cơ số tự nhiên ln(x) là 1/x. Hay nói cách khác:
d(ln x)/dx = 1/x (với x > 0)
Đạo hàm của hàm logarit cơ số a (logax)
Công thức:
Đạo hàm của hàm logarit cơ số a (logax) được tính như sau:
d(logax)/dx = 1/(x ln a) (với x > 0 và a > 0, a ≠ 1)
Ví dụ minh họa
Ví dụ 1:
Tìm đạo hàm của hàm số y = ln(x² + 1).
Sử dụng quy tắc đạo hàm hàm hợp, ta có:
y' = 1/(x² + 1) * d(x² + 1)/dx = 1/(x² + 1) * 2x = 2x/(x² + 1)
Ví dụ 2:
Tìm đạo hàm của hàm số y = log₂(3x).
Áp dụng công thức đạo hàm logarit cơ số a, ta có:
y' = 1/(3x ln 2) * d(3x)/dx = 1/(3x ln 2) * 3 = 1/(x ln 2)
Ứng dụng của đạo hàm logarit
Đạo hàm của hàm logarit có nhiều ứng dụng quan trọng trong toán học và các lĩnh vực khác như:
- Tính toán tốc độ tăng trưởng.
- Giải các bài toán tối ưu hóa.
- Xử lý dữ liệu thống kê.
- Mô hình hóa các hiện tượng tự nhiên.
Hiểu rõ công thức đạo hàm logarit là rất quan trọng để giải quyết các bài toán liên quan đến hàm logarit một cách hiệu quả.
Sản phẩm liên quan: ứng dụng bình thông nhau
Sản phẩm liên quan: viết công thức cấu tạo của axit axetic
Xem thêm: 2 cô gái và 1 cái cốc
Xem thêm: sự im lặng của bầy cừu ý nghĩa
Sản phẩm liên quan: chiếu sáng anh sưởi ấm em truyện