Công thức hạ bậc cos²x

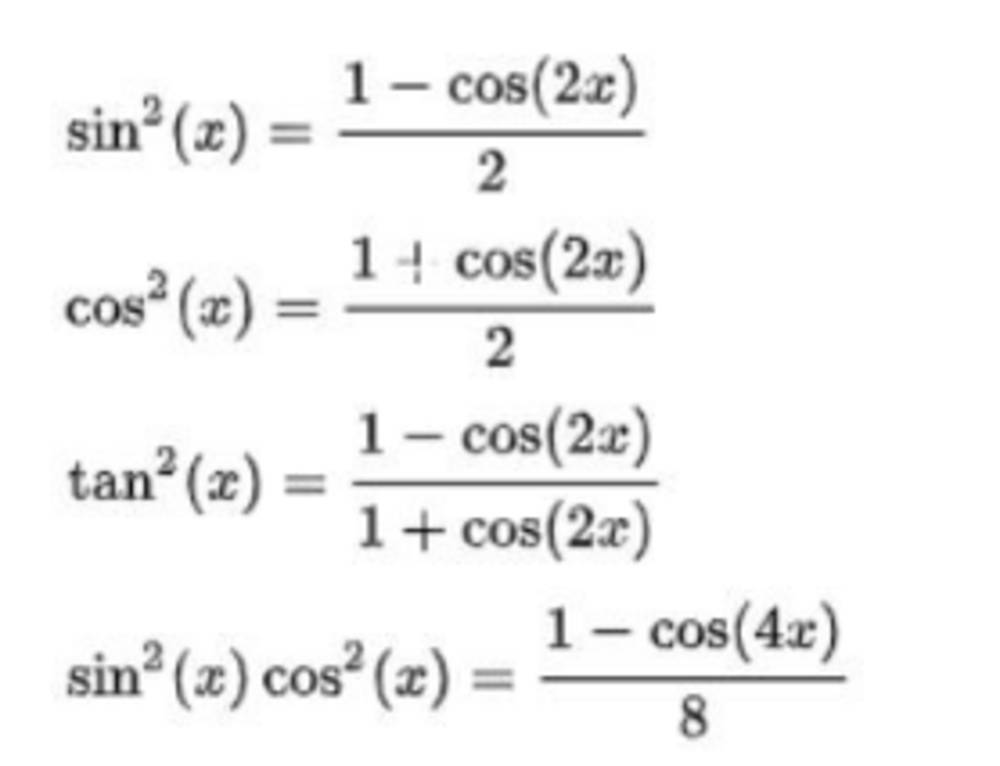

Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Công thức hạ bậc của cos²x là: cos²x = (1 + cos2x)/2. Công thức này giúp biến đổi biểu thức chứa cos²x thành biểu thức chỉ chứa hàm cos với góc nhỏ hơn, đơn giản hóa việc tính toán tích phân, giải phương trình lượng giác và nhiều ứng dụng khác trong toán học.
Chứng minh công thức hạ bậc cos²x
Sử dụng công thức lượng giác cơ bản
Ta bắt đầu từ công thức lượng giác cơ bản: cos2x = cos²(x) - sin²(x). Biết rằng sin²(x) + cos²(x) = 1, ta có sin²(x) = 1 - cos²(x). Thay vào công thức cos2x, ta được: cos2x = cos²(x) - (1 - cos²(x)) = 2cos²(x) - 1. Giải phương trình này cho cos²(x), ta có: 2cos²(x) = 1 + cos2x => cos²(x) = (1 + cos2x)/2.
Sử dụng công thức cộng
Một cách chứng minh khác là sử dụng công thức cộng: cos(a+b) = cos(a)cos(b) - sin(a)sin(b). Cho a = x và b = x, ta có: cos(2x) = cos²(x) - sin²(x). Sử dụng đẳng thức sin²(x) + cos²(x) = 1, ta lại thu được kết quả: cos²(x) = (1 + cos2x)/2.
Ứng dụng của công thức hạ bậc cos²x
Công thức hạ bậc cos²x có nhiều ứng dụng quan trọng trong giải tích và lượng giác, bao gồm:
Tính tích phân
Công thức này giúp đơn giản hóa các tích phân chứa cos²x, làm cho việc tính toán dễ dàng hơn.
Giải phương trình lượng giác
Việc sử dụng công thức hạ bậc giúp đưa phương trình lượng giác về dạng đơn giản hơn, dễ giải hơn.
Đơn giản hóa biểu thức lượng giác
Công thức này giúp làm đơn giản các biểu thức lượng giác phức tạp, thuận tiện cho việc biến đổi và tính toán.
Sản phẩm hữu ích: mụn gạo ở trẻ sơ sinh
Sản phẩm hữu ích: diện tích một mặt hình lập phương
Sản phẩm hữu ích: mẫu hình xăm vòng chân nhật cổ