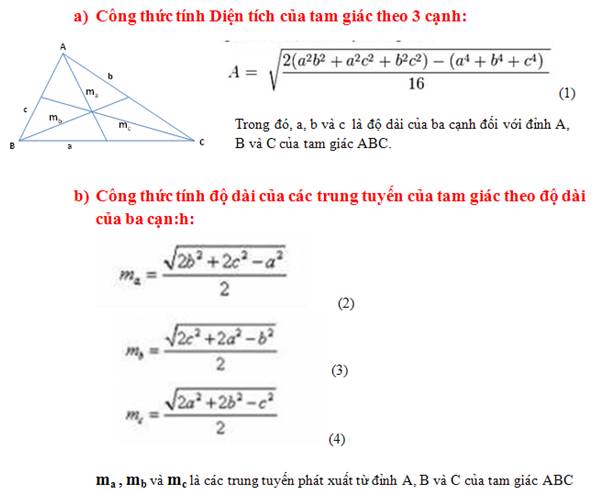
Công thức đường trung tuyến trong tam giác đều cạnh a

Mô tả sản phẩm

Công thức tính đường trung tuyến trong tam giác đều cạnh a là: m = a√3/2, trong đó m là độ dài đường trung tuyến và a là độ dài cạnh của tam giác đều.

Chứng minh công thức đường trung tuyến trong tam giác đều

Sử dụng định lý Pitago

Xét tam giác đều ABC có cạnh a. Gọi M là trung điểm của BC. AM là đường trung tuyến. Ta có BM = MC = a/2. Vì tam giác ABC đều nên AM cũng là đường cao. Trong tam giác vuông AMB, áp dụng định lý Pitago ta có: AM² + BM² = AB² => AM² + (a/2)² = a² => AM² = a² - a²/4 = 3a²/4 => AM = √(3a²/4) = a√3/2. Vậy đường trung tuyến trong tam giác đều cạnh a có độ dài là a√3/2.

Sử dụng tính chất tam giác đều

Trong tam giác đều, đường trung tuyến đồng thời là đường cao và đường phân giác. Do đó, đường trung tuyến chia tam giác đều thành hai tam giác vuông cân. Trong mỗi tam giác vuông cân này, tỉ số giữa cạnh huyền và cạnh góc vuông là √2. Tuy nhiên, ta không thể trực tiếp áp dụng tỉ số này để tính đường trung tuyến. Cách tiếp cận tốt nhất là sử dụng định lý Pitago như đã trình bày ở trên.

Ứng dụng của công thức

Công thức này rất hữu ích trong việc giải các bài toán hình học liên quan đến tam giác đều, giúp tính toán nhanh chóng độ dài đường trung tuyến khi biết độ dài cạnh. Nó được ứng dụng rộng rãi trong các lĩnh vực như xây dựng, thiết kế, và cả trong các bài toán chứng minh hình học phức tạp hơn.

Sản phẩm liên quan: hệ số khuếch tán

Sản phẩm liên quan: toán hình học lớp 8

Xem thêm: động năng là một đại lượng

Xem thêm: al oh 3 naalo2