Công thức đồng biến nghịch biến

Mô tả sản phẩm

Công thức đồng biến nghịch biến phụ thuộc vào loại hàm số bạn đang xét. Đối với hàm số y = f(x), nếu khi x tăng thì y cũng tăng thì hàm số đồng biến, ngược lại nếu x tăng thì y giảm thì hàm số nghịch biến. Để xác định chính xác, ta cần dựa vào đạo hàm của hàm số.

Điều kiện đồng biến và nghịch biến của hàm số

Hàm số y = f(x) xác định trên K

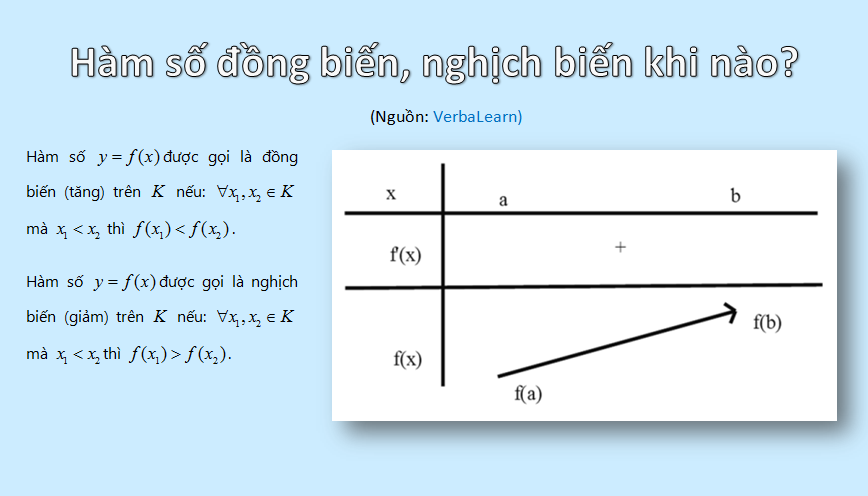
• Đồng biến trên K: ∀x₁, x₂ ∈ K, x₁ < x₂ ⇒ f(x₁) < f(x₂)
• Nghịch biến trên K: ∀x₁, x₂ ∈ K, x₁ < x₂ ⇒ f(x₁) > f(x₂)

Sử dụng đạo hàm để xác định tính đồng biến nghịch biến

• Cho hàm số y = f(x) có đạo hàm trên K.
• Nếu f'(x) > 0 với mọi x ∈ K thì hàm số đồng biến trên K.
• Nếu f'(x) < 0 với mọi x ∈ K thì hàm số nghịch biến trên K.
• Nếu f'(x) = 0 với mọi x ∈ K thì hàm số là hàm hằng trên K (vừa đồng biến vừa nghịch biến).

Lưu ý: Điều kiện f'(x) ≥ 0 hoặc f'(x) ≤ 0 trên K chỉ đủ để kết luận hàm số đồng biến hoặc nghịch biến trên các khoảng con của K, chứ không đủ để kết luận trên toàn bộ K. Cần phải xét thêm các điểm mà đạo hàm bằng 0. Ví dụ: Xét hàm số y = x². Đạo hàm là f'(x) = 2x. Trên khoảng (0, +∞), f'(x) > 0 nên hàm số đồng biến. Trên khoảng (-∞, 0), f'(x) < 0 nên hàm số nghịch biến. Tại x = 0, f'(x) = 0. Tóm lại, việc xác định tính đồng biến hay nghịch biến của một hàm số phụ thuộc vào việc khảo sát đạo hàm của nó. Hiểu rõ các công thức và điều kiện trên sẽ giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.

Sản phẩm hữu ích: thiên an và jack

Xem thêm: 1 lít = dm3

Sản phẩm hữu ích: so sánh tính chất hóa học của nhôm và sắt