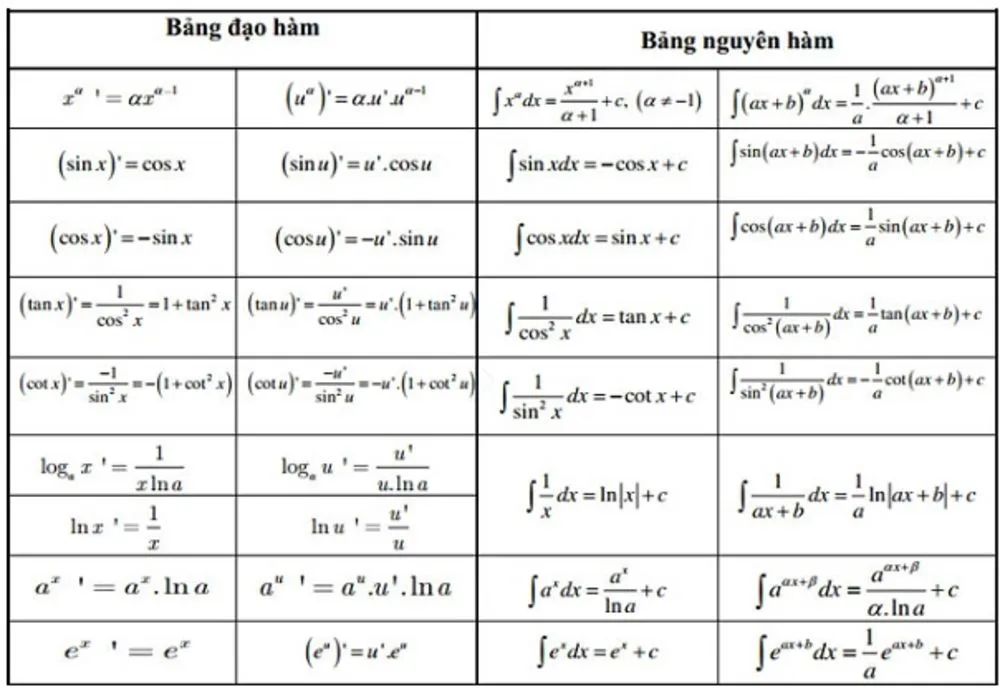
Công thức đạo hàm và nguyên hàm

Mô tả sản phẩm

Bạn đang tìm kiếm công thức đạo hàm và nguyên hàm? Bài viết này sẽ cung cấp cho bạn đầy đủ các công thức đạo hàm và nguyên hàm cơ bản, giúp bạn dễ dàng hiểu và áp dụng vào giải toán. Chúng tôi sẽ trình bày chi tiết từng công thức, kèm theo ví dụ minh họa để bạn nắm vững kiến thức.

Đạo hàm

Định nghĩa đạo hàm

Đạo hàm của một hàm số tại một điểm cho biết tốc độ thay đổi của hàm số tại điểm đó. Nó được định nghĩa như là giới hạn của tỷ số giữa sự thay đổi của hàm số và sự thay đổi của biến số khi sự thay đổi của biến số tiến tới 0. Công thức tổng quát: f'(x) = lim (h→0) [(f(x+h) - f(x))/h].

Các công thức đạo hàm cơ bản

• Đạo hàm của hàm hằng số: d(c)/dx = 0
• Đạo hàm của hàm số xⁿ: d(xⁿ)/dx = nx^n-1
• Đạo hàm của hàm số sin(x): d(sin(x))/dx = cos(x)
• Đạo hàm của hàm số cos(x): d(cos(x))/dx = -sin(x)
• Đạo hàm của hàm số e^x: d(e^x)/dx = e^x
• Đạo hàm của hàm số ln(x): d(ln(x))/dx = 1/x
• Quy tắc đạo hàm tổng: d(f(x) + g(x))/dx = f'(x) + g'(x)
• Quy tắc đạo hàm tích: d(f(x)g(x))/dx = f'(x)g(x) + f(x)g'(x)
• Quy tắc đạo hàm thương: d(f(x)/g(x))/dx = [f'(x)g(x) - f(x)g'(x)] / [g(x)]²
• Đạo hàm hàm hợp: d(f(g(x)))/dx = f'(g(x)) * g'(x)

Nguyên hàm

Định nghĩa nguyên hàm

Nguyên hàm của một hàm số f(x) là một hàm số F(x) sao cho đạo hàm của F(x) bằng f(x), tức là F'(x) = f(x). Nguyên hàm không phải là duy nhất, hai nguyên hàm của cùng một hàm số chỉ khác nhau bởi một hằng số.

Các công thức nguyên hàm cơ bản

• Nguyên hàm của hàm hằng số c: ∫c dx = cx + C
• Nguyên hàm của hàm số xⁿ (n ≠ -1): ∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C
• Nguyên hàm của hàm số sin(x): ∫sin(x) dx = -cos(x) + C
• Nguyên hàm của hàm số cos(x): ∫cos(x) dx = sin(x) + C
• Nguyên hàm của hàm số e^x: ∫e^x dx = e^x + C
• Nguyên hàm của hàm số 1/x: ∫(1/x) dx = ln|x| + C

Lưu ý: C là hằng số tích phân.

Sản phẩm hữu ích: công thức tính diện tích hình tròn có đường kính

Sản phẩm hữu ích: truyền nhiệt đối lưu

Xem thêm: kim loại hoạt động