Chứng minh hai mặt phẳng vuông góc
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
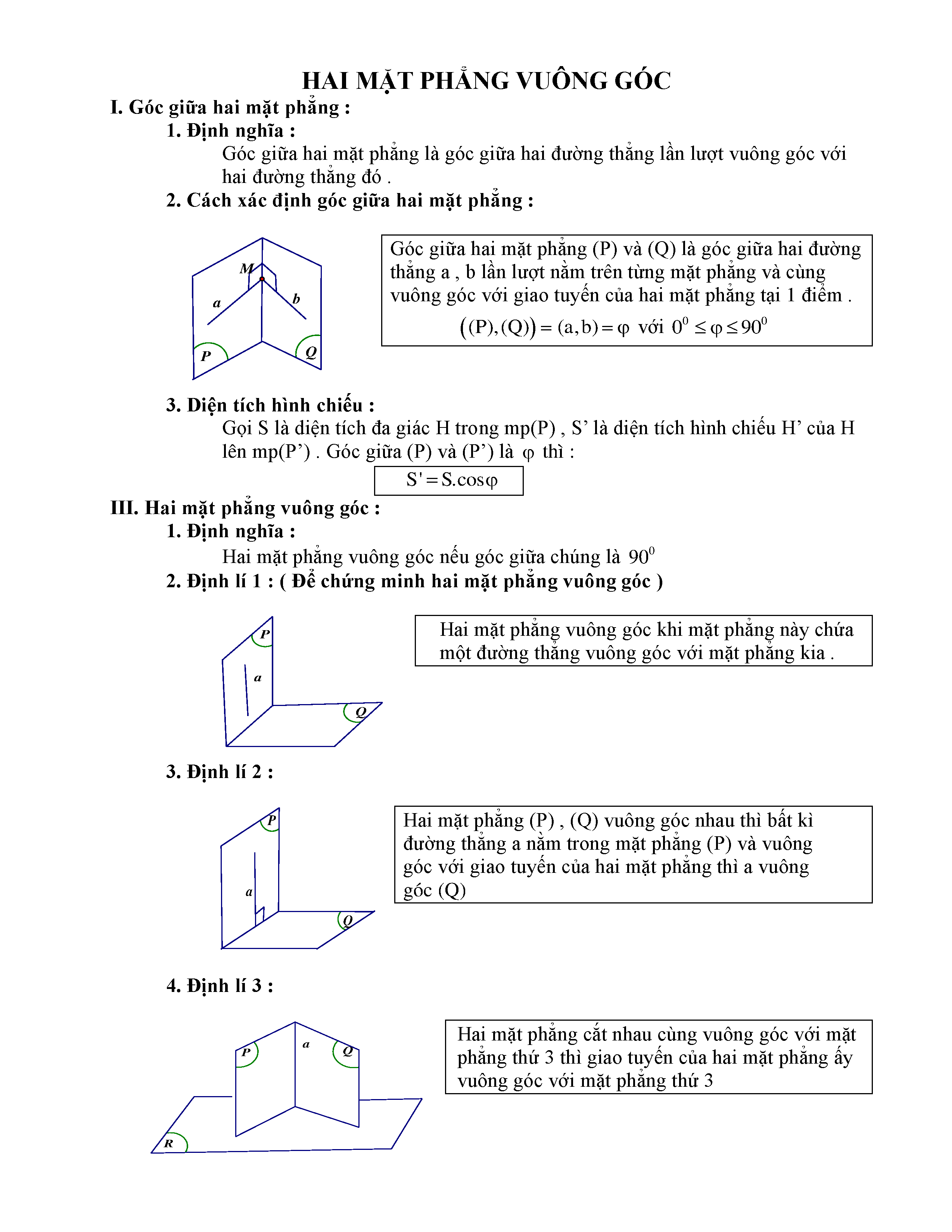
Để chứng minh hai mặt phẳng vuông góc, ta cần chứng minh một mặt phẳng chứa một đường thẳng vuông góc với mặt phẳng kia. Có hai cách chính để chứng minh điều này: chứng minh bằng định nghĩa hoặc chứng minh dựa trên các tính chất của đường thẳng và mặt phẳng vuông góc.
Phương pháp 1: Chứng minh bằng định nghĩa
Định nghĩa hai mặt phẳng vuông góc
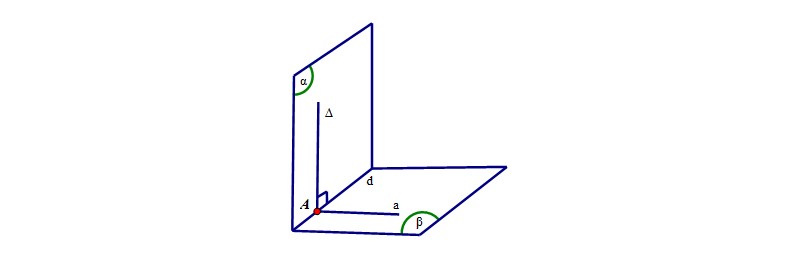
Hai mặt phẳng được gọi là vuông góc với nhau nếu một mặt phẳng chứa một đường thẳng vuông góc với mặt phẳng kia. Tức là, nếu mặt phẳng (α) chứa đường thẳng a vuông góc với mặt phẳng (β) (a ⊥ (β)), thì ta kết luận (α) ⊥ (β).
Áp dụng định nghĩa để chứng minh
Để áp dụng định nghĩa này, ta cần tìm một đường thẳng nằm trong mặt phẳng này và vuông góc với mặt phẳng kia. Việc tìm đường thẳng này phụ thuộc vào hình học cụ thể của bài toán. Thông thường, ta sẽ sử dụng các kiến thức về hình học không gian, như tính chất của các hình chóp, hình lăng trụ, hay các hệ thức lượng trong tam giác để tìm đường thẳng cần thiết. Sau khi tìm được đường thẳng đó, ta cần chứng minh đường thẳng đó vuông góc với mặt phẳng kia bằng cách chứng minh nó vuông góc với hai đường thẳng cắt nhau trong mặt phẳng đó.
Phương pháp 2: Chứng minh dựa trên các tính chất
Các tính chất quan trọng
Ngoài định nghĩa, ta có thể sử dụng các tính chất sau để chứng minh hai mặt phẳng vuông góc:
- Nếu hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.
- Nếu một mặt phẳng chứa một đường thẳng vuông góc với một mặt phẳng khác thì hai mặt phẳng đó vuông góc với nhau.
- Nếu hai mặt phẳng vuông góc thì góc giữa bất kỳ đường thẳng nào nằm trong mặt phẳng này với mặt phẳng kia sẽ bằng 90 độ.
Áp dụng các tính chất để chứng minh
Tùy thuộc vào bài toán cụ thể, ta có thể chọn lựa các tính chất phù hợp để chứng minh hai mặt phẳng vuông góc. Ví dụ, nếu ta biết hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba, ta có thể sử dụng tính chất đầu tiên để kết luận về sự vuông góc của hai mặt phẳng đó. Hoặc nếu ta tìm được một đường thẳng nằm trong một mặt phẳng và vuông góc với mặt phẳng kia, ta có thể sử dụng tính chất thứ hai để chứng minh hai mặt phẳng vuông góc.
Sản phẩm hữu ích: nhà nở hậu chữ l
Sản phẩm liên quan: cách tính tốc độ
Xem thêm: mấy ngày nữa đi học
Sản phẩm liên quan: dấu hiệu nhận biết hbh
Sản phẩm liên quan: naoh ra nước gia ven