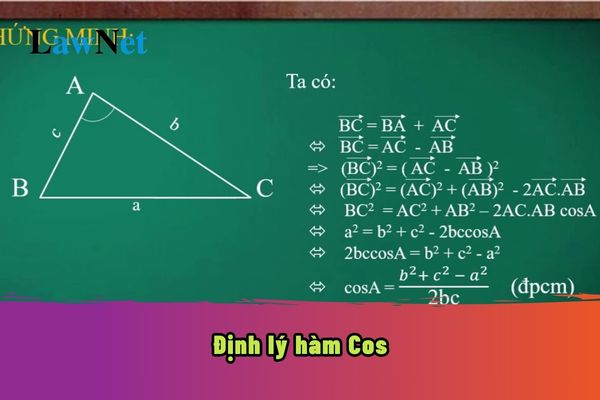
Chứng minh Định lý Cosin lớp 9

Mô tả sản phẩm

Bạn đang tìm cách chứng minh định lý Cosin cho tam giác lớp 9? Bài viết này sẽ hướng dẫn bạn cách chứng minh định lý một cách chi tiết và dễ hiểu nhất. Định lý Cosin khẳng định rằng trong một tam giác bất kỳ, bình phương của một cạnh bằng tổng bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với Cosin của góc xen giữa.

Định lý Cosin là gì?

Phát biểu định lý

Trong tam giác ABC, ta có: a² = b² + c² - 2bc.cosA b² = a² + c² - 2ac.cosB c² = a² + b² - 2ab.cosC (với a, b, c lần lượt là độ dài các cạnh đối diện với các góc A, B, C)

Chứng minh Định lý Cosin

Phương pháp chứng minh

Ta sẽ chứng minh công thức a² = b² + c² - 2bc.cosA. Hai công thức còn lại chứng minh tương tự. Xét tam giác ABC. Kẻ đường cao AH (H thuộc BC). * Trường hợp H nằm giữa B và C: Trong tam giác vuông AHB, ta có: AH² = c² - BH² Trong tam giác vuông AHC, ta có: AH² = b² - CH² Suy ra: c² - BH² = b² - CH² => c² - b² = BH² - CH² Ta có: BH = c - CH. Do đó, BH² - CH² = (c - CH)² - CH² = c² - 2c.CH + CH² - CH² = c² - 2c.CH Vậy c² - b² = c² - 2c.CH => b² = 2c.CH Trong tam giác AHC, ta có: CH = b.cosC => b² = 2c.b.cosC => b = 2c.cosC Từ tam giác AHB, ta có: BH = c.cosB Từ tam giác AHC, ta có: CH = b.cosC Ta có: a = BH + CH = c.cosB + b.cosC Áp dụng định lý Pytago cho tam giác AHB: AB² = AH² + BH² Áp dụng định lý Pytago cho tam giác AHC: AC² = AH² + CH² Từ đó ta suy ra a² = b² + c² - 2bc.cosA * Trường hợp H trùng B hoặc C hoặc H nằm ngoài BC: Chứng minh tương tự, chỉ khác ở việc biểu diễn BH và CH.

Sản phẩm liên quan: tác dụng của lực là gì

Sản phẩm hữu ích: thuật toán tìm kiếm tuần tự thực hiện công việc

Sản phẩm liên quan: máy phát điện xoay chiều có mấy bộ phận chính