Chứng minh công thức gia tốc hướng tâm

Mô tả sản phẩm

Công thức gia tốc hướng tâm là a_ht = v²/r = ω²r, trong đó v là vận tốc dài, r là bán kính quỹ đạo và ω là vận tốc góc. Để chứng minh công thức này, ta cần hiểu rõ khái niệm gia tốc và vận tốc trong chuyển động tròn đều.

Chuyển động tròn đều và vectơ vận tốc

Đặc điểm của chuyển động tròn đều

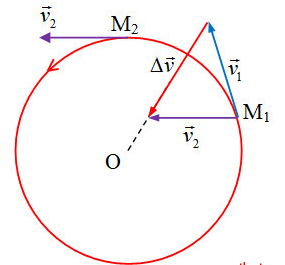
Chuyển động tròn đều là chuyển động có quỹ đạo là đường tròn và có tốc độ không đổi. Mặc dù tốc độ không đổi, nhưng vận tốc lại liên tục thay đổi vì hướng của vận tốc luôn tiếp tuyến với quỹ đạo và thay đổi theo thời gian.

Sự thay đổi của vectơ vận tốc

Xét một vật chuyển động tròn đều với vận tốc v. Trong một khoảng thời gian ngắn Δt, vật di chuyển từ điểm A đến điểm B trên đường tròn. Vận tốc tại A là v_A và vận tốc tại B là v_B. Cả hai vectơ vận tốc này đều có độ lớn bằng v nhưng hướng khác nhau. Sự thay đổi vận tốc Δv = v_B - v_A chính là đại lượng cho biết sự thay đổi hướng của vận tốc.

Chứng minh công thức gia tốc hướng tâm

Phân tích vectơ thay đổi vận tốc

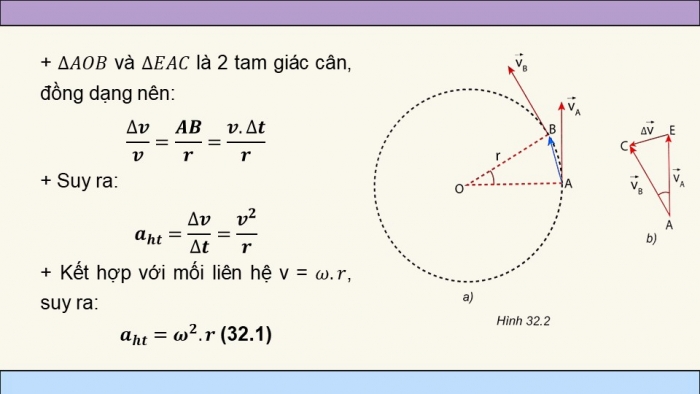
Nếu khoảng thời gian Δt rất nhỏ, thì cung AB gần như là một đoạn thẳng. Ta có thể coi tam giác tạo bởi v_A, v_B và Δv là một tam giác cân với hai cạnh bằng v. Góc ở đỉnh của tam giác này bằng Δθ (góc quét được trong thời gian Δt). Do đó, độ lớn của Δv có thể tính gần đúng bằng: |Δv| ≈ vΔθ.

Gia tốc trung bình và gia tốc tức thời

Gia tốc trung bình trong khoảng thời gian Δt là: a_tb = |Δv|/Δt ≈ vΔθ/Δt. Khi Δt tiến đến 0, gia tốc trung bình trở thành gia tốc tức thời a_ht. Vì Δθ/Δt = ω (vận tốc góc), ta có: a_ht = vω.

Kết luận

Vì v = ωr, thay vào công thức trên, ta được hai dạng của công thức gia tốc hướng tâm: a_ht = v²/r = ω²r. Gia tốc hướng tâm luôn hướng về tâm của đường tròn, do đó nó được gọi là gia tốc hướng tâm.

Xem thêm: vật liệu cao su

Sản phẩm hữu ích: ch3coona + hcl có xảy ra không

Xem thêm: kí hiệu cung mọc