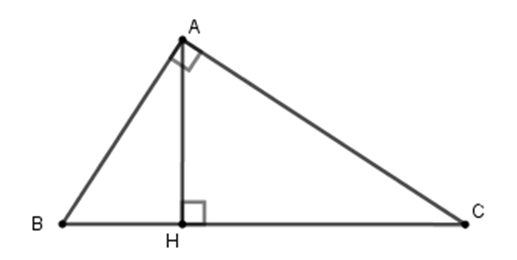
Tam giác ABC vuông tại A (AB < AC), đường cao AH

Mô tả sản phẩm

Cho tam giác ABC vuông tại A với AB < AC và đường cao AH. Bài viết này sẽ giúp bạn hiểu rõ hơn về các tính chất và mối quan hệ giữa các cạnh và các góc trong tam giác vuông này, cũng như cách áp dụng định lý Pitago và các hệ thức lượng trong tam giác vuông để giải quyết các bài toán liên quan.

Các hệ thức lượng trong tam giác vuông ABC

Định lý Pitago:

Trong tam giác ABC vuông tại A, ta có:
BC² = AB² + AC²
Đây là hệ thức cơ bản nhất giúp tính độ dài cạnh huyền khi biết độ dài hai cạnh góc vuông.

Hệ thức giữa cạnh góc vuông và hình chiếu:

AB² = BH.BC
AC² = CH.BC
AH² = BH.CH
Những hệ thức này cho phép tính độ dài các cạnh khi biết độ dài của một cạnh và hình chiếu của nó trên cạnh huyền.

Hệ thức giữa đường cao và các cạnh:

AH.BC = AB.AC
Đây là hệ thức liên hệ giữa đường cao AH với các cạnh của tam giác.

Ứng dụng của các hệ thức lượng

Các hệ thức lượng trong tam giác vuông được ứng dụng rộng rãi trong giải toán hình học, đặc biệt là trong các bài toán liên quan đến tính toán độ dài các cạnh, góc, diện tích của tam giác vuông. Việc nắm vững các hệ thức này giúp giải quyết nhanh chóng và chính xác các bài toán phức tạp. Ví dụ, ta có thể tính được độ dài đường cao, độ dài các cạnh, diện tích tam giác,... khi biết một số thông tin ban đầu.

Bài tập ví dụ

(Thêm các bài tập ví dụ minh họa ở đây, kèm lời giải)

Sản phẩm liên quan: điện một chiều là gì

Sản phẩm liên quan: giải bài tập sgk toán 11 kết nối tri thức

Xem thêm: hoa cúc khô mua ở tiệm thuốc bắc

Sản phẩm hữu ích: cách tính tiền giảm theo phần trăm

Sản phẩm hữu ích: đa thức nội suy newton