Cách Tính Tập Nghiệm Của Bất Phương Trình
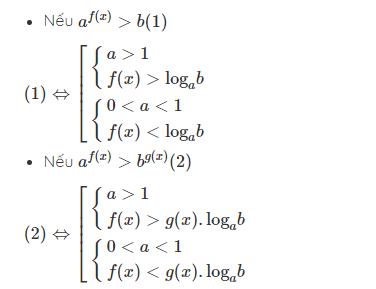


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Để tìm tập nghiệm của bất phương trình, bạn cần thực hiện các bước biến đổi tương đương để cô lập biến, sau đó biểu diễn kết quả trên trục số hoặc dùng ký hiệu tập hợp. Phương pháp cụ thể phụ thuộc vào loại bất phương trình.
Các Loại Bất Phương Trình và Cách Giải
Bất Phương Trình Bậc Nhất Một Ẩn
Bất phương trình bậc nhất một ẩn có dạng ax + b > 0, ax + b < 0, ax + b ≥ 0, ax + b ≤ 0 (với a ≠ 0). Để giải, bạn thực hiện các bước sau:- Chuyển các số hạng không chứa x sang vế phải.
- Chia cả hai vế cho a (nếu a > 0 thì giữ nguyên dấu bất phương trình, nếu a < 0 thì đổi chiều dấu bất phương trình).
- Viết tập nghiệm dưới dạng khoảng, đoạn hoặc nửa khoảng trên trục số.
- 2x > 7 - 3
- 2x > 4
- x > 2
Bất Phương Trình Bậc Hai Một Ẩn
Bất phương trình bậc hai một ẩn có dạng ax² + bx + c > 0, ax² + bx + c < 0, ax² + bx + c ≥ 0, ax² + bx + c ≤ 0 (với a ≠ 0). Để giải, bạn cần:- Tìm nghiệm của phương trình ax² + bx + c = 0 (nếu có).
- Xét dấu của tam thức bậc hai ax² + bx + c dựa vào bảng xét dấu hoặc đồ thị hàm số y = ax² + bx + c.
- Dựa vào dấu của tam thức và dấu của bất phương trình để xác định tập nghiệm.
Bất Phương Trình Mũ và Logarit
Giải bất phương trình mũ và logarit thường đòi hỏi kiến thức về tính chất của hàm mũ và hàm logarit. Cần sử dụng các tính chất để biến đổi bất phương trình về dạng đơn giản hơn, sau đó tìm tập nghiệm. Điều quan trọng là luôn chú ý đến điều kiện xác định của bất phương trình.Bất Phương Trình chứa dấu giá trị tuyệt đối
Để giải bất phương trình chứa dấu giá trị tuyệt đối, ta cần xét các trường hợp khác nhau để loại bỏ dấu giá trị tuyệt đối, sau đó giải các bất phương trình thu được và hợp nghiệm lại. Tóm lại, việc tìm tập nghiệm của bất phương trình đòi hỏi sự hiểu biết rõ ràng về các loại bất phương trình và các kỹ thuật giải tương ứng. Luôn nhớ kiểm tra lại kết quả để đảm bảo tính chính xác.Sản phẩm liên quan: muối kép là gì
Sản phẩm hữu ích: trong tiến hóa các cơ quan tương tự có ý nghĩa phản ánh
Sản phẩm liên quan: khả năng nhịn ăn của chó
Sản phẩm liên quan: điều chế isoamyl axetat