Cách Tính Tam Giác Cân

Mô tả sản phẩm

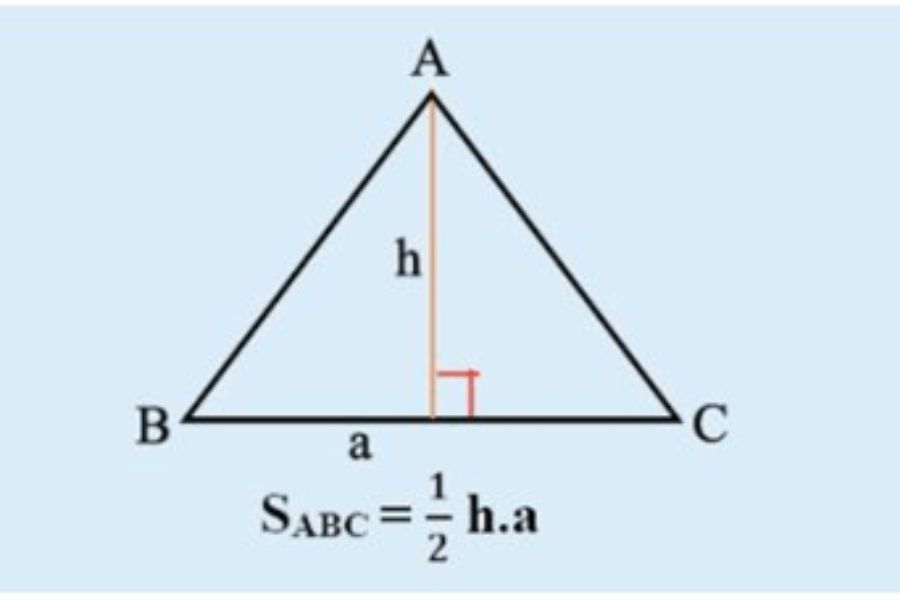
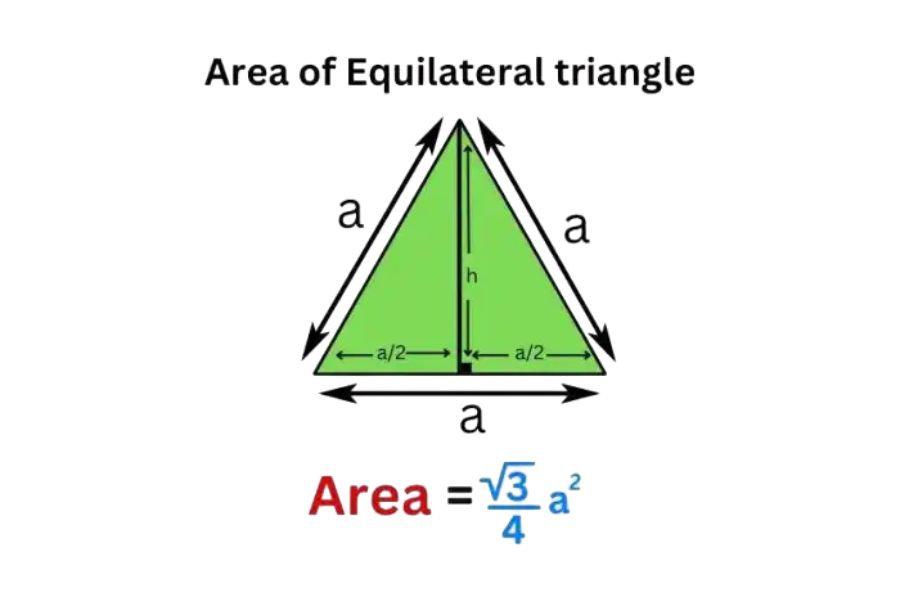
Cách tính tam giác cân phụ thuộc vào dữ liệu đã biết. Bạn cần biết ít nhất ba yếu tố (cạnh, góc) để tính toán các yếu tố còn lại. Ví dụ, nếu biết hai cạnh bằng nhau và góc xen giữa, bạn có thể tính được cạnh còn lại và các góc còn lại. Tương tự, nếu biết một cạnh và hai góc, bạn cũng có thể tính được các yếu tố còn lại.

Các Trường Hợp Tính Tam Giác Cân

1. Biết hai cạnh bằng nhau và góc xen giữa:

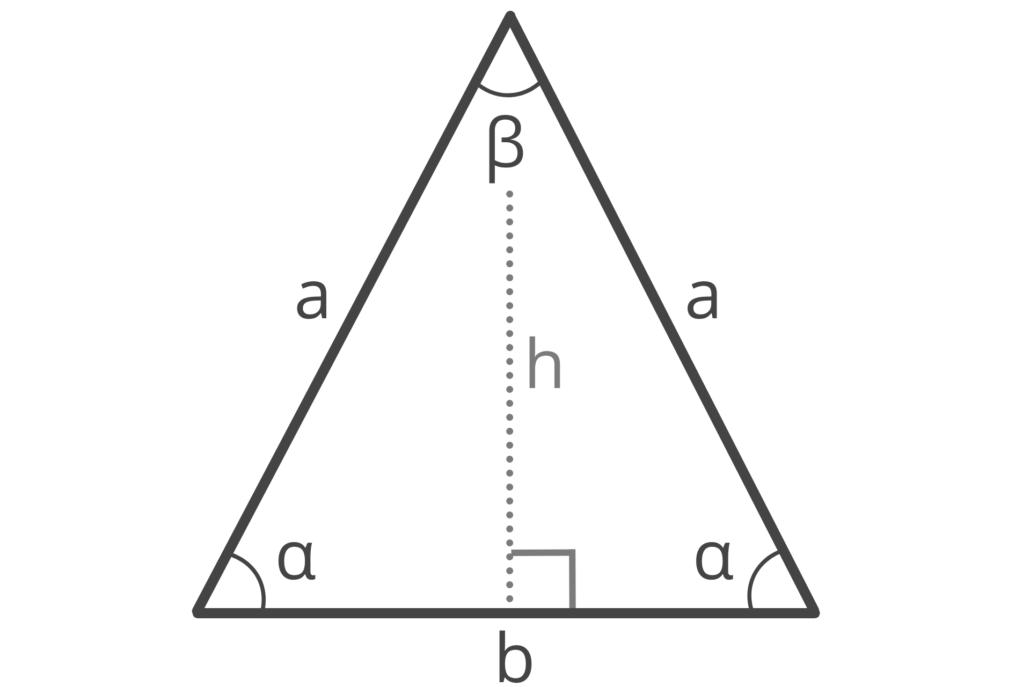
Để tính toán các yếu tố còn lại, bạn sử dụng định lý cosin và định lý sin. Giả sử tam giác ABC cân tại A, với AB = AC = a và góc BAC = α. Ta có: * BC = 2a*sin(α/2) (định lý sin) * Góc ABC = Góc ACB = (180° - α)/2

2. Biết một cạnh và hai góc:

Vì tổng ba góc trong tam giác bằng 180°, bạn dễ dàng tính được góc thứ ba. Sau đó, sử dụng định lý sin để tính độ dài hai cạnh còn lại. Giả sử bạn biết cạnh AB = c, góc BAC = α và góc ABC = β. Ta có: * Góc ACB = 180° - α - β * AC = c*sin(β)/sin(α) * BC = c*sin(180° - α - β)/sin(α)

3. Biết hai cạnh bằng nhau và một góc khác:

Nếu biết hai cạnh bằng nhau (AB = AC = a) và một góc khác (ví dụ góc ABC = β), bạn có thể tính góc còn lại (góc ACB = β) và cạnh đáy BC bằng định lý sin.

4. Biết cạnh đáy và một góc:

Nếu bạn biết cạnh đáy (BC) và một góc (ví dụ góc ABC = β), trường hợp này cần thêm thông tin để giải. Bạn cần biết ít nhất một yếu tố khác nữa như độ dài một cạnh bên hoặc một góc khác. Lưu ý: Trong các trường hợp trên, bạn cần sử dụng các công thức lượng giác cơ bản như định lý sin, định lý cosin. Bạn có thể sử dụng máy tính hoặc các phần mềm toán học để hỗ trợ tính toán. Hiểu rõ các tính chất của tam giác cân sẽ giúp bạn dễ dàng lựa chọn phương pháp tính toán phù hợp.

Sản phẩm hữu ích: cặp học sinh lớp 1 cho be trai

Sản phẩm hữu ích: công thức tính số vòng dây lớp 9

Sản phẩm liên quan: ảnh của một vật thật tạo bởi thấu kính phân kì luôn là

Sản phẩm liên quan: công thức khối lập phương

Xem thêm: alcl3 dư + naoh