Cách Tính Q1, Q2, Q3

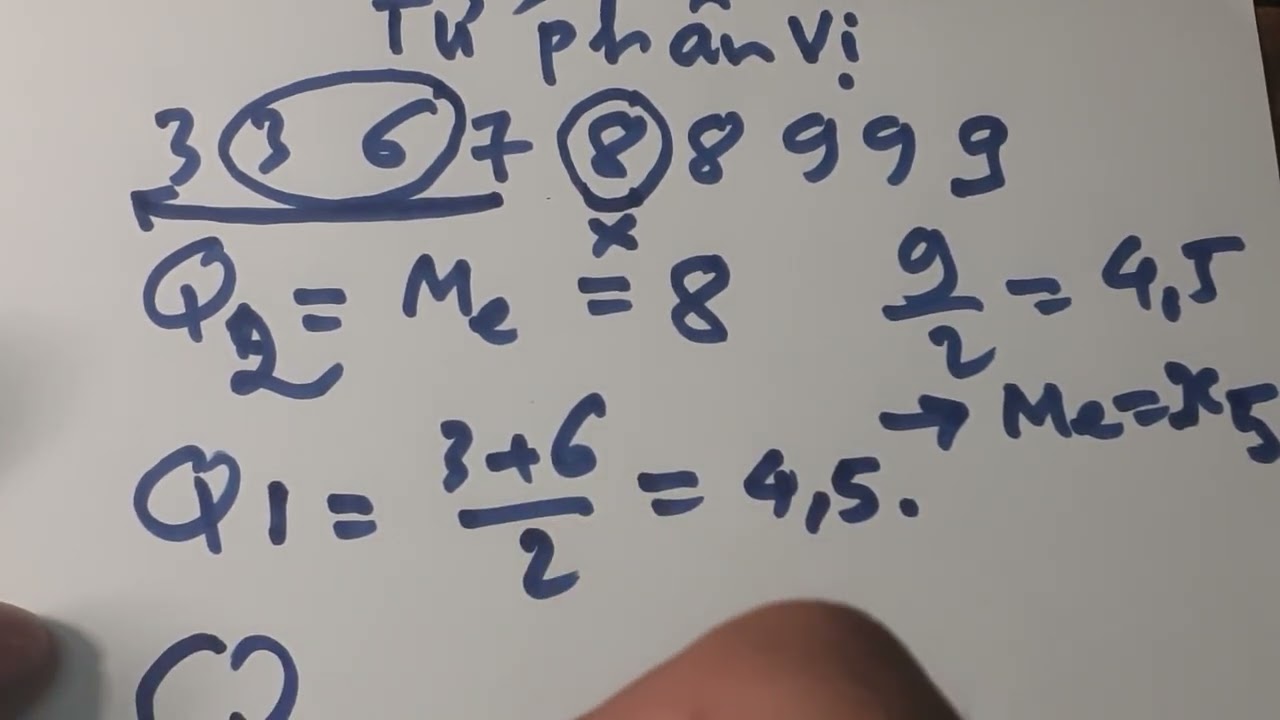
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
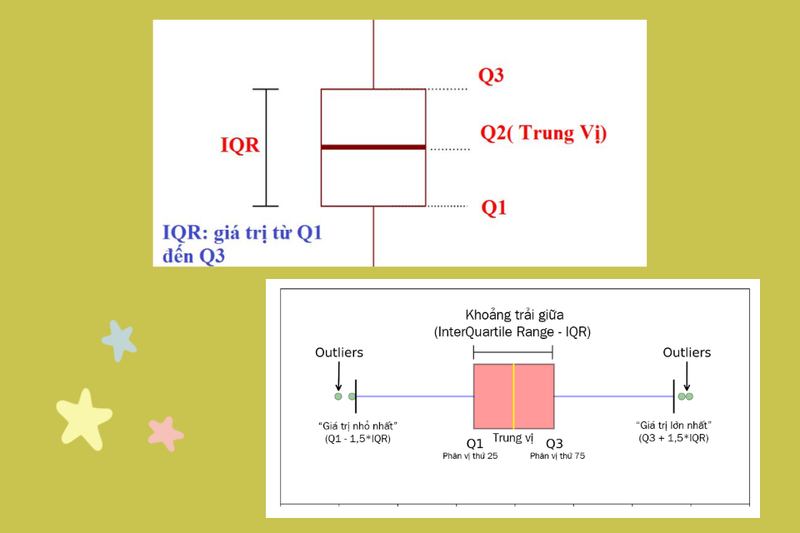
Q1, Q2, và Q3 là các tứ phân vị, chia một tập dữ liệu đã được sắp xếp thành bốn phần bằng nhau. Q2 chính là trung vị của toàn bộ tập dữ liệu. Q1 là trung vị của nửa dữ liệu nằm bên dưới Q2, và Q3 là trung vị của nửa dữ liệu nằm trên Q2. Vậy làm thế nào để tính chúng? Hãy cùng tìm hiểu.
Cách tính Q1, Q2, Q3
Tính Q2 (Trung vị)
Để tính Q2, trước tiên bạn cần sắp xếp dữ liệu theo thứ tự tăng dần. Nếu số lượng dữ liệu là số lẻ, Q2 là giá trị ở giữa. Nếu số lượng dữ liệu là số chẵn, Q2 là trung bình cộng của hai giá trị ở giữa. Ví dụ: Tập dữ liệu {2, 5, 8, 10, 12, 15}. Số lượng dữ liệu là 6 (số chẵn). Q2 = (8 + 10) / 2 = 9.Tính Q1
Sau khi tìm được Q2, ta chia tập dữ liệu thành hai nửa: nửa dưới (các giá trị nhỏ hơn hoặc bằng Q2) và nửa trên (các giá trị lớn hơn hoặc bằng Q2). Q1 là trung vị của nửa dữ liệu dưới. Nếu số lượng dữ liệu trong nửa dưới là số lẻ, Q1 là giá trị ở giữa. Nếu số lượng dữ liệu là số chẵn, Q1 là trung bình cộng của hai giá trị ở giữa. Ví dụ (tiếp tục ví dụ trên): Nửa dưới là {2, 5, 8}. Q1 = 5.Tính Q3
Tương tự, Q3 là trung vị của nửa dữ liệu trên. Ví dụ (tiếp tục ví dụ trên): Nửa trên là {10, 12, 15}. Q3 = 12.Ví dụ minh họa
Giả sử ta có tập dữ liệu sau: {1, 3, 5, 7, 9, 11, 13}. * **Q2 (Trung vị):** Dữ liệu đã được sắp xếp, số lượng dữ liệu là 7 (số lẻ), Q2 = 7. * **Q1:** Nửa dưới: {1, 3, 5}. Q1 = 3. * **Q3:** Nửa trên: {9, 11, 13}. Q3 = 11. Tóm lại, việc tính Q1, Q2, Q3 khá đơn giản nếu bạn hiểu rõ khái niệm trung vị và cách chia tập dữ liệu thành các phần bằng nhau. Hiểu được các tứ phân vị giúp bạn phân tích dữ liệu hiệu quả hơn, đặc biệt là trong việc hiểu rõ sự phân bố của dữ liệu và phát hiện các ngoại lệ.Sản phẩm hữu ích: 9 thước bằng bao nhiêu mét
Sản phẩm hữu ích: nai sừng tấm tiếng anh
Sản phẩm liên quan: đom đóm vào nhà báo hiệu điều gì
Xem thêm: vẽ voi ma mút