Cách tính đường cao trong tam giác đều

Mô tả sản phẩm

Cách tính đường cao trong tam giác đều rất đơn giản. Đường cao của tam giác đều có độ dài bằng a√3/2, trong đó a là độ dài cạnh của tam giác.

Công thức tính đường cao tam giác đều

Công thức tổng quát

Với a là độ dài cạnh của tam giác đều, đường cao h được tính theo công thức: h = a√3/2

Ví dụ minh họa

Giả sử ta có một tam giác đều có cạnh a = 6cm. Để tính đường cao h, ta áp dụng công thức:

h = 6√3/2 = 3√3 cm ≈ 5.196 cm

Chứng minh công thức

Sử dụng định lý Pytago

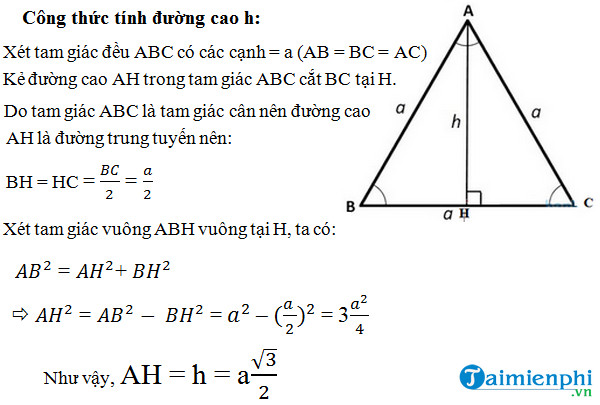
Trong tam giác đều, đường cao cũng chính là đường trung tuyến, chia cạnh đáy thành hai phần bằng nhau. Xét một nửa tam giác đều, ta có một tam giác vuông với hai cạnh góc vuông là a/2 (nửa cạnh đáy) và h (đường cao), và cạnh huyền là a. Áp dụng định lý Pytago, ta có:

(a/2)² + h² = a²

h² = a² - (a/2)² = a² - a²/4 = 3a²/4

h = √(3a²/4) = a√3/2

Sử dụng lượng giác

Trong tam giác đều, mỗi góc đều bằng 60 độ. Xét một nửa tam giác đều, ta có một tam giác vuông. Sử dụng lượng giác, ta có:

sin(60°) = h/a

h = a * sin(60°) = a * (√3/2) = a√3/2

Sản phẩm liên quan: công thức cấu tạo thu gọn của rượu etylic là

Sản phẩm liên quan: mốt của mẫu số liệu ghép nhóm

Sản phẩm liên quan: vbt toán lớp 3 chân trời sáng tạo

Sản phẩm liên quan: lá lành dùm lá rách

Sản phẩm liên quan: viết công thức cấu tạo của axit axetic