Cách Tính Độ Lệch Chuẩn
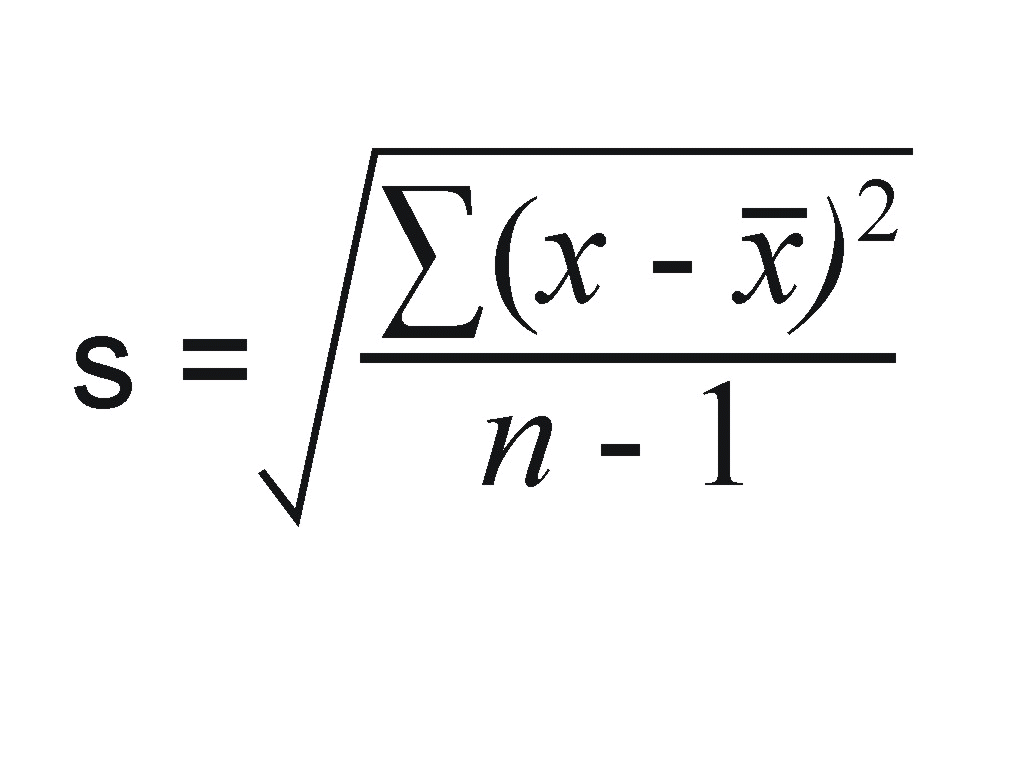
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
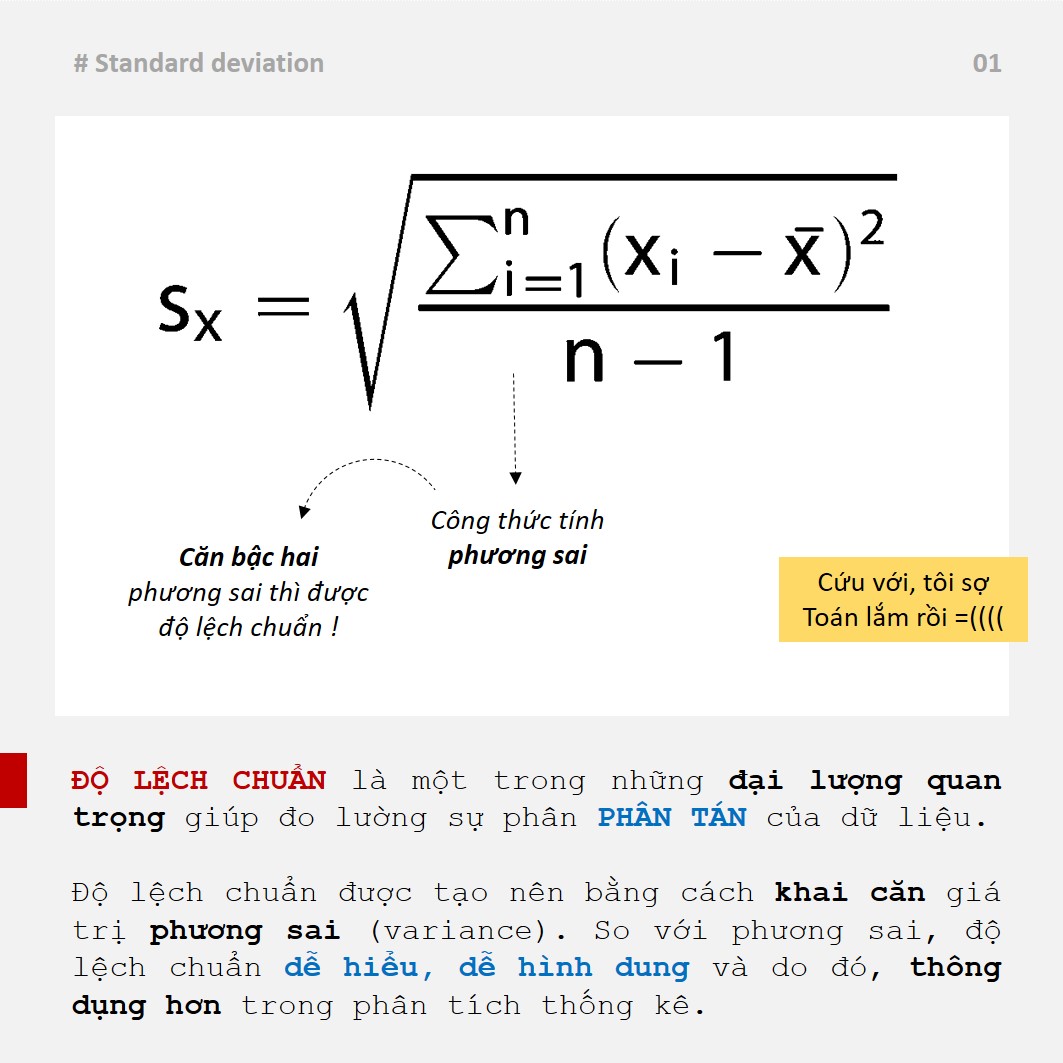
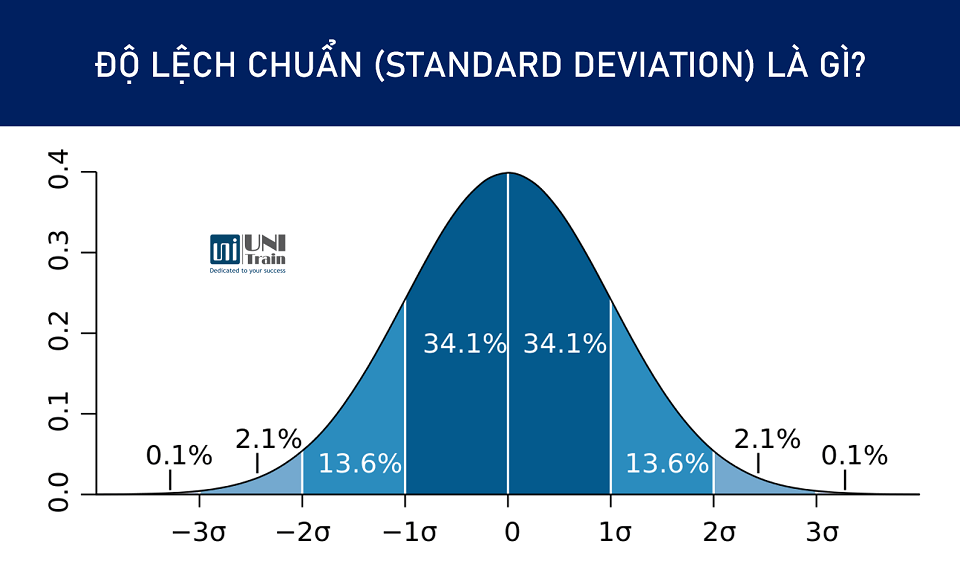
Độ lệch chuẩn là một thước đo thống kê phản ánh mức độ phân tán của dữ liệu so với giá trị trung bình. Một độ lệch chuẩn nhỏ cho thấy dữ liệu tập trung quanh giá trị trung bình, trong khi độ lệch chuẩn lớn cho thấy dữ liệu phân tán rộng hơn.
Công thức Tính Độ Lệch Chuẩn
Độ lệch chuẩn mẫu (Sample Standard Deviation)
Công thức tính độ lệch chuẩn mẫu được sử dụng khi bạn đang làm việc với một mẫu dữ liệu, chứ không phải toàn bộ quần thể. Công thức như sau: s = √[Σ(xi - x̄)² / (n - 1)] Trong đó: * s là độ lệch chuẩn mẫu. * xi là giá trị quan sát thứ i. * x̄ là giá trị trung bình mẫu. * n là số lượng quan sát trong mẫu. * Σ là ký hiệu tổng. (n-1) được sử dụng thay vì n để điều chỉnh độ lệch chuẩn mẫu cho việc ước lượng độ lệch chuẩn quần thể.Độ lệch chuẩn quần thể (Population Standard Deviation)
Nếu bạn đang làm việc với toàn bộ quần thể dữ liệu, công thức tính độ lệch chuẩn quần thể là: σ = √[Σ(xi - μ)² / N] Trong đó: * σ là độ lệch chuẩn quần thể. * xi là giá trị quan sát thứ i. * μ là giá trị trung bình quần thể. * N là tổng số quan sát trong quần thể.Ví dụ Minh Họa
Giả sử chúng ta có một mẫu dữ liệu gồm các số liệu sau: 2, 4, 4, 4, 5, 5, 7, 9. 1. **Tính giá trị trung bình mẫu (x̄):** (2 + 4 + 4 + 4 + 5 + 5 + 7 + 9) / 8 = 5 2. **Tính tổng bình phương độ lệch:** (2-5)² + (4-5)² + (4-5)² + (4-5)² + (5-5)² + (5-5)² + (7-5)² + (9-5)² = 20 3. **Tính phương sai mẫu:** 20 / (8 - 1) = 2.86 4. **Tính độ lệch chuẩn mẫu (s):** √2.86 ≈ 1.69 Do đó, độ lệch chuẩn mẫu của tập dữ liệu này là khoảng 1.69.Ứng dụng của Độ Lệch Chuẩn
Độ lệch chuẩn có nhiều ứng dụng quan trọng trong thống kê và các lĩnh vực khác, bao gồm: * **Đánh giá độ phân tán dữ liệu:** Cho thấy mức độ tập trung hoặc phân tán của dữ liệu xung quanh giá trị trung bình. * **So sánh các tập dữ liệu khác nhau:** Giúp so sánh mức độ biến động của các tập dữ liệu. * **Kiểm định giả thuyết thống kê:** Được sử dụng trong nhiều kiểm định thống kê để đánh giá ý nghĩa thống kê của kết quả. * **Quản lý chất lượng:** Đánh giá độ chính xác và ổn định của quá trình sản xuất.Xem thêm: naoh + nahso4
Xem thêm: phản ứng nào là phản ứng oxi hóa khử
Sản phẩm hữu ích: al2(so4)3+naoh=al(oh)3+na2so4 balance the equation