Cách tìm tập xác định

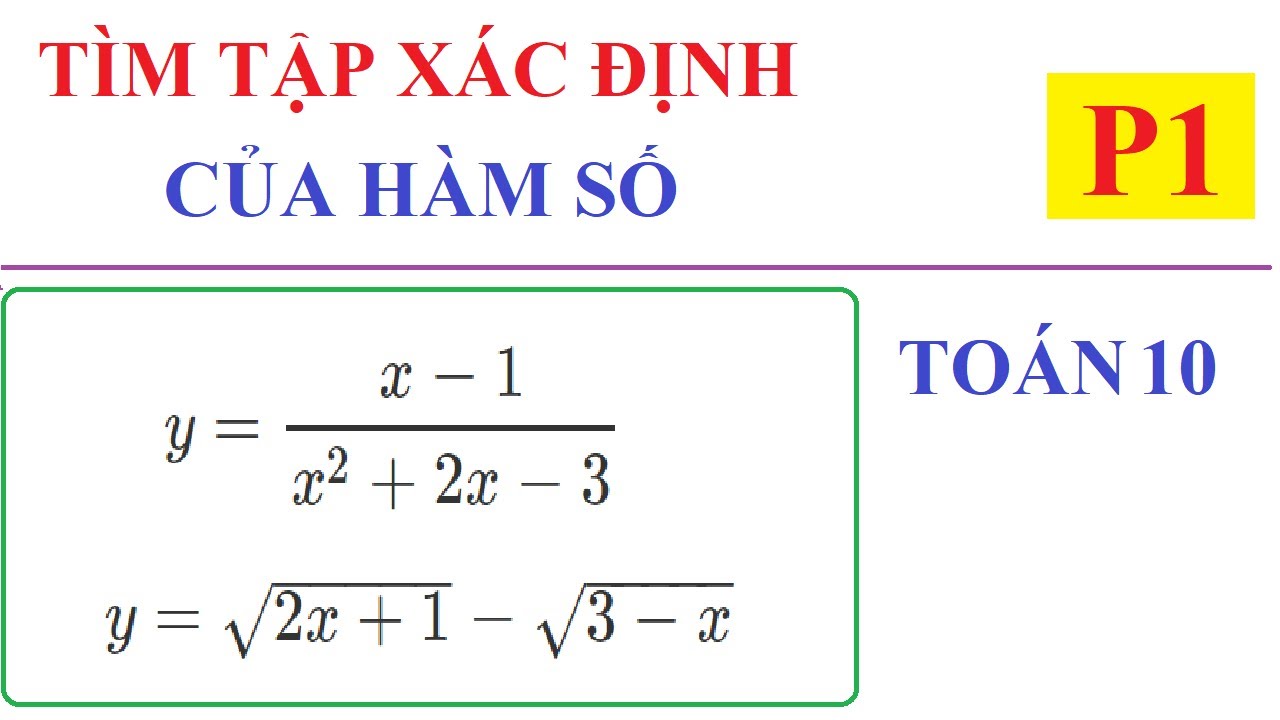
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Tập xác định của một hàm số là tập hợp tất cả các giá trị của biến số độc lập x sao cho hàm số có nghĩa. Để tìm tập xác định, bạn cần xét các điều kiện để biểu thức hàm số tồn tại và có giá trị thực.
Các bước tìm tập xác định
Điều kiện 1: Mẫu số khác 0
Nếu hàm số có dạng f(x) = a/b(x), với b(x) là biểu thức chứa x ở mẫu số, thì điều kiện để hàm số có nghĩa là b(x) ≠ 0. Bạn cần giải bất phương trình b(x) ≠ 0 để tìm tập xác định.
Điều kiện 2: Biểu thức trong căn bậc chẵn không âm
Nếu hàm số có dạng f(x) = √g(x), với g(x) là biểu thức chứa x nằm trong căn bậc chẵn (căn bậc hai, căn bậc bốn, ...), thì điều kiện để hàm số có nghĩa là g(x) ≥ 0. Bạn cần giải bất phương trình g(x) ≥ 0 để tìm tập xác định.
Điều kiện 3: Biểu thức logarit có cơ số dương khác 1 và đối số dương
Nếu hàm số có dạng f(x) = logag(x), với a là cơ số và g(x) là đối số, thì điều kiện để hàm số có nghĩa là a > 0, a ≠ 1 và g(x) > 0. Bạn cần giải hệ bất phương trình a > 0, a ≠ 1 và g(x) > 0 để tìm tập xác định.
Điều kiện 4: Hàm số lượng giác
Đối với các hàm số lượng giác như tanx, cotx, thì cần chú ý đến các giá trị làm cho hàm số không xác định. Ví dụ: tanx không xác định khi cosx = 0, cotx không xác định khi sinx = 0.
Ví dụ:
Tìm tập xác định của hàm số f(x) = √(x-2) / (x-3).
Để hàm số có nghĩa, ta cần thỏa mãn hai điều kiện:
- Biểu thức trong căn không âm: x - 2 ≥ 0 => x ≥ 2
- Mẫu số khác 0: x - 3 ≠ 0 => x ≠ 3
Sản phẩm hữu ích: kí tự dễ thương con thỏ
Xem thêm: công thức tính điện thế tại 1 điểm
Sản phẩm liên quan: toán xác suất thống kê lớp 11
Sản phẩm hữu ích: nguyên liệu để sản xuất canxi oxit là