Cách Tìm Ma Trận Khả Nghịch

Mô tả sản phẩm

Để tìm xem một ma trận có khả nghịch hay không và tìm ma trận nghịch đảo của nó, ta cần dựa vào định thức và các phép biến đổi hàng. Một ma trận vuông khả nghịch khi và chỉ khi định thức của nó khác 0. Nếu định thức khác 0, ta có thể tìm ma trận nghịch đảo bằng phương pháp dùng định thức hoặc phương pháp khử Gauss-Jordan.

Phương pháp dùng định thức

Tính định thức

Trước tiên, ta cần tính định thức của ma trận. Nếu định thức bằng 0, ma trận không khả nghịch và dừng lại ở đây. Nếu định thức khác 0, ta tiến hành bước tiếp theo.

Tìm ma trận phụ hợp

Tiếp theo, ta tìm ma trận phụ hợp (adjoint matrix) của ma trận ban đầu. Ma trận phụ hợp được tạo thành từ các phần bù đại số của các phần tử trong ma trận. Phần bù đại số của một phần tử là định thức của ma trận con thu được bằng cách loại bỏ hàng và cột chứa phần tử đó, nhân với (-1)^(i+j), trong đó i và j là chỉ số hàng và cột của phần tử.

Tính ma trận nghịch đảo

Cuối cùng, ma trận nghịch đảo được tính bằng cách chia ma trận phụ hợp cho định thức của ma trận ban đầu. A^-1 = (1/det(A)) * adj(A), trong đó A^-1 là ma trận nghịch đảo, det(A) là định thức của A và adj(A) là ma trận phụ hợp của A.

Phương pháp khử Gauss-Jordan

Tạo ma trận mở rộng

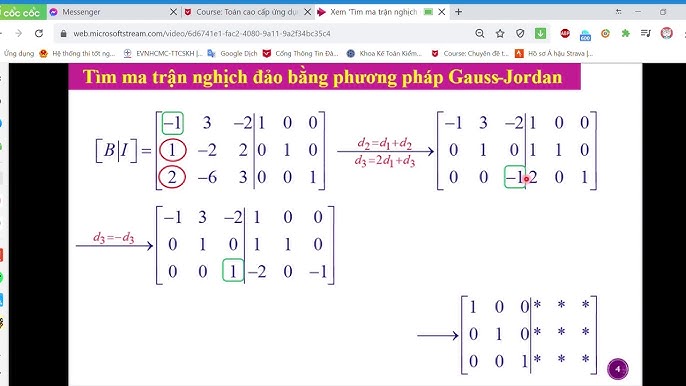
Phương pháp này liên quan đến việc tạo một ma trận mở rộng bằng cách nối ma trận ban đầu với ma trận đơn vị cùng kích thước.

Khử Gauss-Jordan

Áp dụng các phép biến đổi hàng cơ bản (đổi chỗ hai hàng, nhân một hàng với một số khác 0, cộng một bội số của một hàng vào một hàng khác) để biến ma trận ban đầu thành ma trận đơn vị. Những phép biến đổi này cũng được áp dụng đồng thời cho ma trận đơn vị ở phía bên phải.

Kết quả

Sau khi thực hiện khử Gauss-Jordan, phần ma trận ban đầu đã trở thành ma trận đơn vị, và phần ma trận đơn vị ban đầu sẽ trở thành ma trận nghịch đảo của ma trận ban đầu.

Sản phẩm liên quan: câu nói nổi tiếng của joker

Xem thêm: cắt tóc mái theo khuôn mặt

Sản phẩm liên quan: câu chuyện về ngô quyền