Cách Chứng Minh Trọng Tâm
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
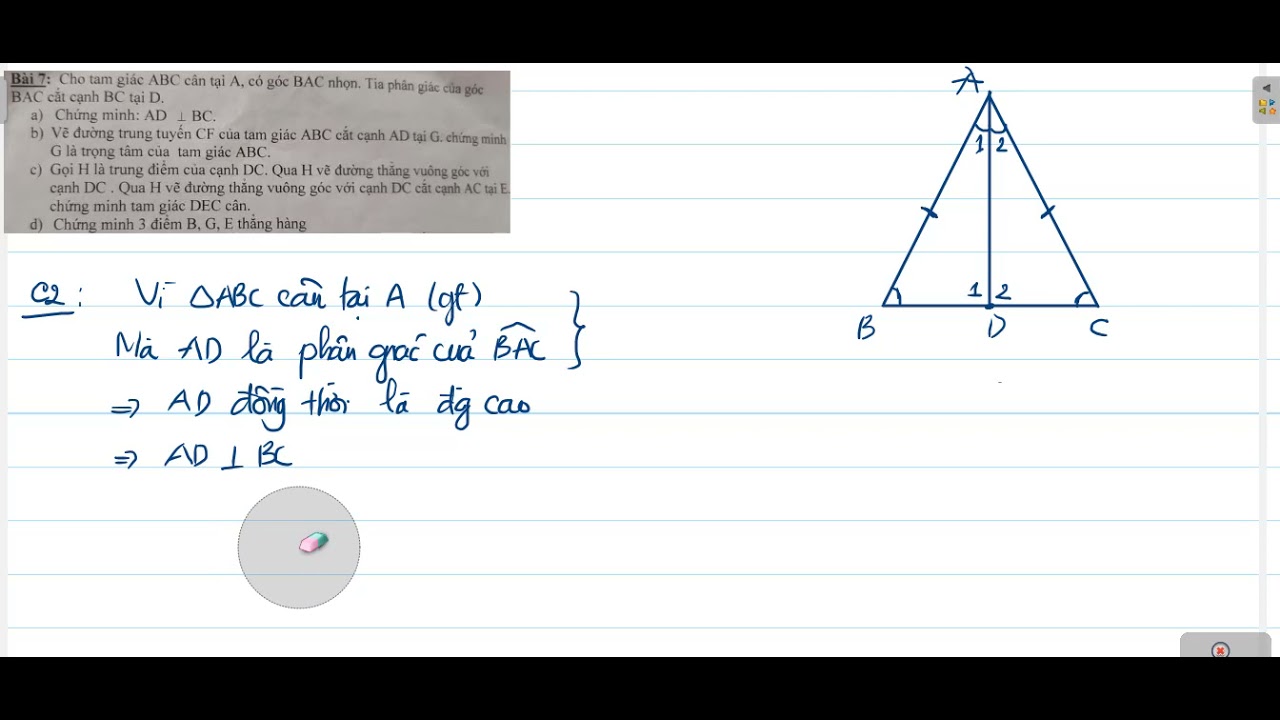
Để chứng minh một điểm là trọng tâm của một tam giác, bạn cần chứng minh điểm đó là giao điểm của hai trong ba đường trung tuyến của tam giác đó. Hay nói cách khác, bạn cần chứng minh điểm đó cách đều hai đỉnh của tam giác và nằm trên đường thẳng nối đỉnh còn lại với trung điểm của cạnh đối diện.
Phương pháp chứng minh trọng tâm
Chứng minh bằng định nghĩa
Định nghĩa trọng tâm là giao điểm của ba đường trung tuyến trong một tam giác. Để chứng minh điểm G là trọng tâm của tam giác ABC, ta cần chứng minh G là giao điểm của ít nhất hai đường trung tuyến. Ví dụ: Chứng minh G nằm trên đường trung tuyến AM và BN. Điều này có thể được thực hiện bằng cách sử dụng tính chất của các đường trung tuyến, ví dụ như tỉ số giữa các đoạn thẳng tạo bởi trọng tâm và các đỉnh hoặc trung điểm.
Chứng minh bằng tọa độ
Nếu biết tọa độ các đỉnh của tam giác, ta có thể xác định tọa độ trọng tâm bằng công thức: G( (xA + xB + xC)/3, (yA + yB + yC)/3 ). Sau khi tìm được tọa độ trọng tâm, ta có thể sử dụng các công thức về đường thẳng và khoảng cách để chứng minh điểm đó nằm trên các đường trung tuyến.
Chứng minh bằng vectơ
Sử dụng tính chất vectơ của trọng tâm: 
, trong đó $\vec{OA} + \vec{OB} + \vec{OC} = 3\vec{OG}$ với O là một điểm bất kỳ, A, B, C là các đỉnh của tam giác, và G là trọng tâm. Từ công thức này, ta có thể suy ra vị trí của G so với các đỉnh và trung điểm của các cạnh.
Ví dụ minh họa
Giả sử ta có tam giác ABC với A(1,2), B(3,4), C(5,6). Ta có thể tính tọa độ trọng tâm G bằng công thức: G((1+3+5)/3, (2+4+6)/3) = G(3,4). Sau đó, ta có thể chứng minh G nằm trên các đường trung tuyến bằng cách tính phương trình đường thẳng của các đường trung tuyến và kiểm tra xem G có thuộc các đường thẳng đó hay không.
Kết luận
Có nhiều cách để chứng minh một điểm là trọng tâm của tam giác, tùy thuộc vào thông tin đã biết và phương pháp chứng minh phù hợp. Việc lựa chọn phương pháp sẽ phụ thuộc vào dữ kiện bài toán.
Sản phẩm hữu ích: bánh ướt tiếng anh là gì
Sản phẩm liên quan: vẽ thuyền buồm trên biển
Sản phẩm hữu ích: dap noi ban sat di hoc
Xem thêm: vinyl fomat