Cách Chứng Minh Trọng Tâm Của Tam Giác

Mô tả sản phẩm

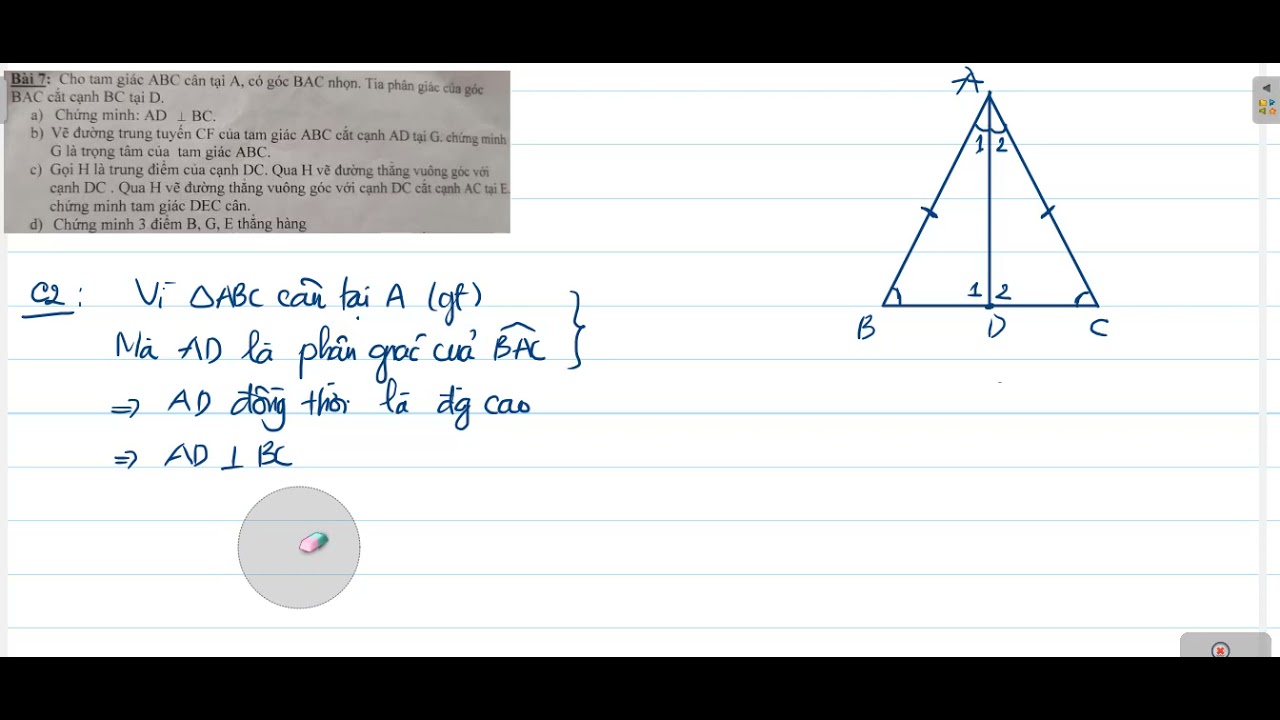
Trọng tâm của tam giác là điểm giao nhau của ba đường trung tuyến. Để chứng minh một điểm là trọng tâm, ta cần chứng minh điểm đó nằm trên cả ba đường trung tuyến. Có nhiều cách chứng minh, tùy thuộc vào kiến thức đã học và dữ kiện cho trước.

Phương pháp chứng minh sử dụng tọa độ

Sử dụng công thức trung điểm và trọng tâm

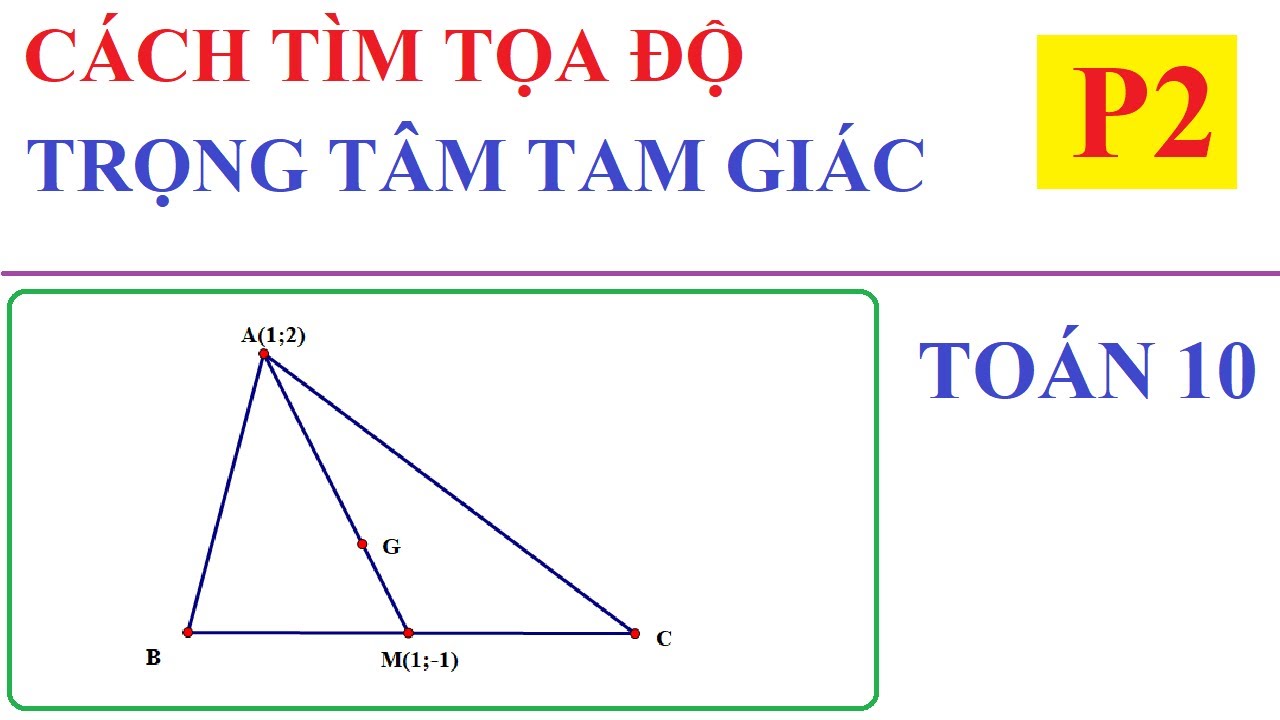
Giả sử tam giác ABC có tọa độ các đỉnh A(x_A, y_A), B(x_B, y_B), C(x_C, y_C). Trung điểm M của AB có tọa độ: M($\frac{x_A + x_B}{2}$, $\frac{y_A + y_B}{2}$). Trung tuyến CM đi qua C và M. Tương tự, ta tìm được trung điểm N của AC và trung tuyến BN. Trọng tâm G có tọa độ: G($\frac{x_A + x_B + x_C}{3}$, $\frac{y_A + y_B + y_C}{3}$). Để chứng minh một điểm là trọng tâm, ta chỉ cần kiểm tra xem tọa độ điểm đó có thỏa mãn công thức trọng tâm hay không.

Vecto

Sử dụng phép cộng vecto. Cho G là trọng tâm của tam giác ABC. Khi đó, ta có:
$\vec{GA} + \vec{GB} + \vec{GC} = \vec{0}$
Từ đó, ta có thể chứng minh ngược lại: nếu một điểm G thỏa mãn đẳng thức trên thì G là trọng tâm của tam giác ABC. Đây là một cách chứng minh ngắn gọn và hiệu quả.

Phương pháp chứng minh hình học

Sử dụng định lý Menelaus và Ceva

Đây là phương pháp chứng minh khá phức tạp, yêu cầu kiến thức về hình học phẳng sâu hơn. Định lý Menelaus và Ceva được sử dụng để chứng minh tính đồng quy của ba đường trung tuyến.

Tổng kết

Có nhiều cách để chứng minh trọng tâm của tam giác. Việc lựa chọn phương pháp phù hợp phụ thuộc vào dữ kiện bài toán và kiến thức đã học. Các phương pháp trên đều cho kết quả chính xác và giúp ta hiểu rõ hơn về tính chất của trọng tâm trong tam giác.

Sản phẩm liên quan: khối lượng nguyên tử trung bình

Xem thêm: cách để học giỏi toán hình lớp 8

Xem thêm: tính chất đặc trưng của kim loại là

Xem thêm: văn nghị luận về câu tục ngữ có công mài sắt có ngày nên kim