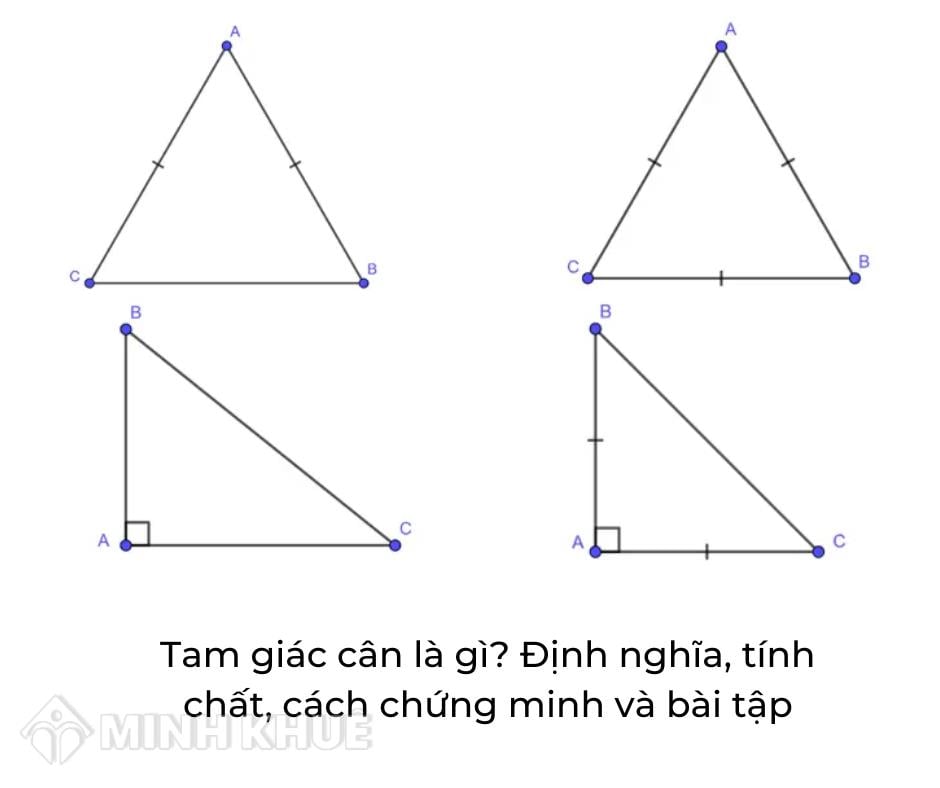
Cách Chứng Minh Tam Giác Cân Lớp 8

Mô tả sản phẩm

Để chứng minh một tam giác là tam giác cân ở lớp 8, bạn cần dựa vào định nghĩa và các tính chất của tam giác cân, cùng với các kiến thức về tam giác đã học. Có nhiều cách chứng minh, tùy thuộc vào dữ kiện bài toán cho. Dưới đây là một số cách phổ biến:

1. Chứng minh dựa vào định nghĩa

1.1 Định nghĩa tam giác cân:

Tam giác cân là tam giác có hai cạnh bằng nhau. Nếu chứng minh được hai cạnh của một tam giác bằng nhau, thì tam giác đó là tam giác cân.

1.2 Áp dụng:

Ví dụ: Cho tam giác ABC. Nếu bạn chứng minh được AB = AC ( bằng cách sử dụng các tính chất như cạnh đối diện với góc bằng nhau, hoặc bằng cách sử dụng các trường hợp bằng nhau của tam giác), thì tam giác ABC là tam giác cân tại A.

2. Chứng minh dựa vào tính chất

2.1 Tính chất tam giác cân:

Trong một tam giác cân, hai góc ở đáy bằng nhau. Ngược lại, nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

2.2 Áp dụng:

Ví dụ: Cho tam giác ABC. Nếu bạn chứng minh được ∠B = ∠C ( bằng cách sử dụng các tính chất về góc, hoặc bằng cách sử dụng các trường hợp bằng nhau của tam giác), thì tam giác ABC là tam giác cân tại A.

3. Chứng minh dựa vào trường hợp bằng nhau của tam giác

3.1 Các trường hợp bằng nhau:

Bạn có thể sử dụng các trường hợp bằng nhau của hai tam giác (c.c.c, c.g.c, g.c.g) để chứng minh hai cạnh hoặc hai góc của tam giác bằng nhau, từ đó suy ra tam giác đó là tam giác cân.

3.2 Áp dụng:

Ví dụ: Cho tam giác ABC và tam giác A'B'C'. Nếu bạn chứng minh được ∆ABC = ∆A'B'C' (bằng một trong các trường hợp bằng nhau), và biết A'B'C' là tam giác cân, thì tam giác ABC cũng là tam giác cân. Tóm lại, để chứng minh một tam giác là tam giác cân lớp 8, bạn cần linh hoạt vận dụng định nghĩa, tính chất và các trường hợp bằng nhau của tam giác để tìm ra cách chứng minh phù hợp nhất với từng bài toán. Hãy nhớ phân tích kỹ đề bài và lựa chọn phương pháp chứng minh sao cho hợp lý và chính xác.

Sản phẩm liên quan: hoc tieng anh lop 2

Xem thêm: ma cương thi cute

Sản phẩm hữu ích: kể về một kỉ niệm đáng nhớ với người thân ngắn gọn