Cách Chứng Minh 4 Điểm Cùng Thuộc 1 Đường Tròn

Mô tả sản phẩm

Để chứng minh 4 điểm cùng thuộc một đường tròn, ta cần chứng minh chúng thỏa mãn một trong các điều kiện sau đây. Bài viết này sẽ hướng dẫn bạn chi tiết các cách chứng minh đó.

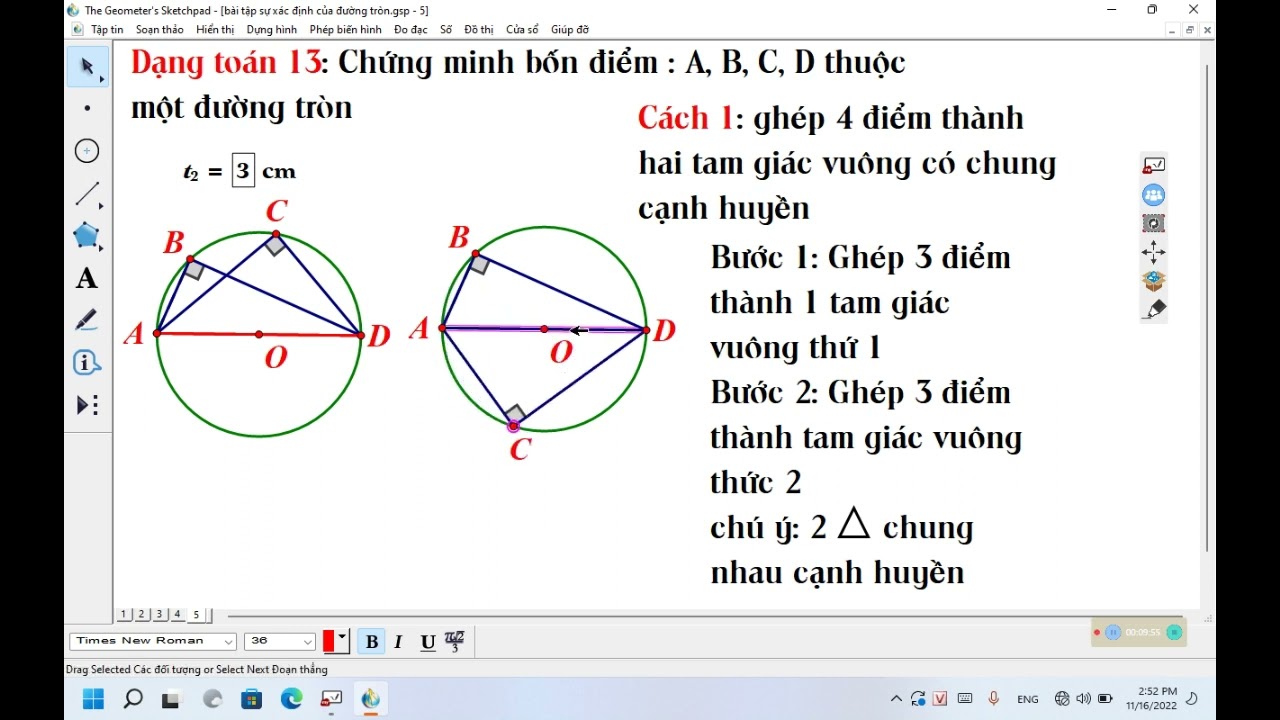
Các phương pháp chứng minh 4 điểm cùng thuộc 1 đường tròn

1. Sử dụng tính chất góc nội tiếp

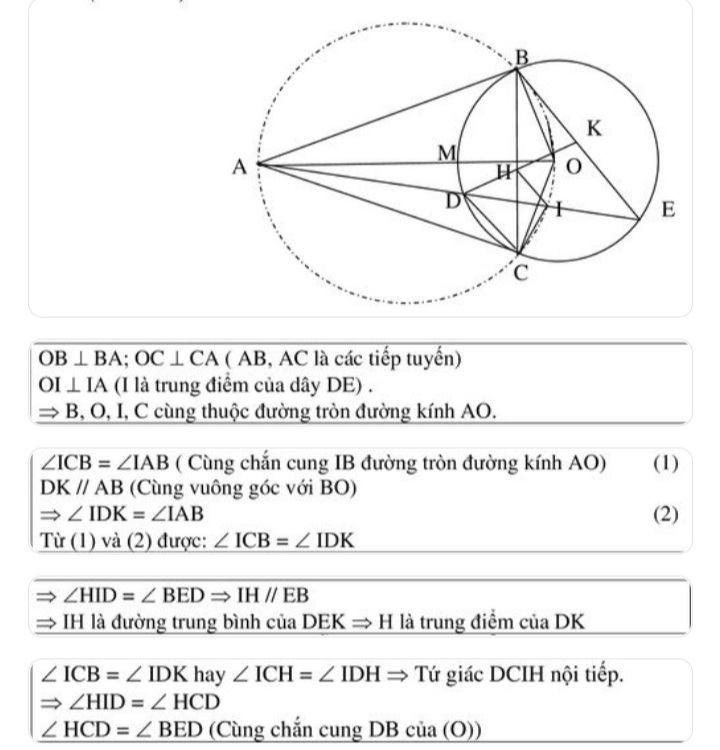
Để chứng minh 4 điểm A, B, C, D cùng thuộc một đường tròn, ta có thể chứng minh rằng: góc tạo bởi hai dây cung AB và CD cùng chắn một cung, hoặc góc ở tâm bằng 2 lần góc nội tiếp cùng chắn một cung. Nếu góc nội tiếp cùng chắn một cung có số đo bằng nhau thì 4 điểm đó cùng nằm trên một đường tròn. Ví dụ: Nếu ∠ABC = ∠ADC (hai góc nội tiếp cùng chắn cung AC), thì A, B, C, D cùng thuộc một đường tròn.

2. Sử dụng định lý về đường tròn ngoại tiếp tứ giác

Một tứ giác nội tiếp được đường tròn khi và chỉ khi tổng hai góc đối diện bằng 180 độ. Nếu chứng minh được tổng hai góc đối diện của tứ giác ABCD (ví dụ ∠ABC + ∠ADC = 180°) bằng 180 độ, thì ta kết luận được rằng A, B, C, D cùng nằm trên một đường tròn.

3. Sử dụng phương pháp vecto

Phương pháp này phức tạp hơn và thường được sử dụng trong các bài toán nâng cao. Chứng minh rằng tích vô hướng của hai vecto tạo bởi các điểm A, B, C, D thỏa mãn một điều kiện đặc biệt, từ đó suy ra 4 điểm cùng thuộc một đường tròn. Đây là phương pháp đòi hỏi kiến thức về vecto sâu hơn.

4. Sử dụng tâm đường tròn

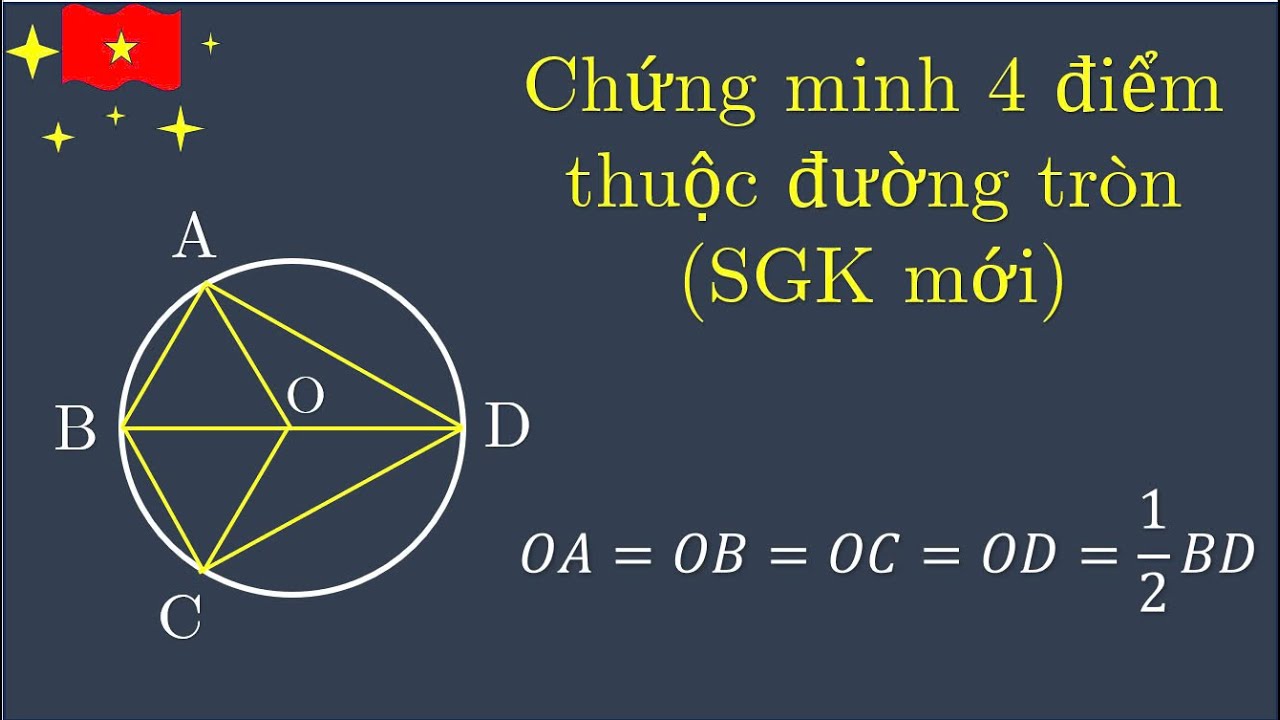
Nếu tìm được một điểm O sao cho OA = OB = OC = OD (tất cả các khoảng cách từ O đến 4 điểm đều bằng nhau), thì O chính là tâm của đường tròn đi qua 4 điểm A, B, C, D. Tức là 4 điểm này cùng nằm trên đường tròn tâm O. Tuy nhiên, phương pháp này thường khó áp dụng trong thực tế do việc tìm tâm đường tròn không phải lúc nào cũng dễ dàng.

Sản phẩm hữu ích: nghe chep chinh ta

Sản phẩm hữu ích: kính cha diệp 9 lần

Sản phẩm hữu ích: bài tập toán 9 chương 1

Xem thêm: tiếng hót của chào mào

Sản phẩm hữu ích: đề thi công nghệ lớp 3 kết nối tri thức