Hằng đẳng thức mở rộng
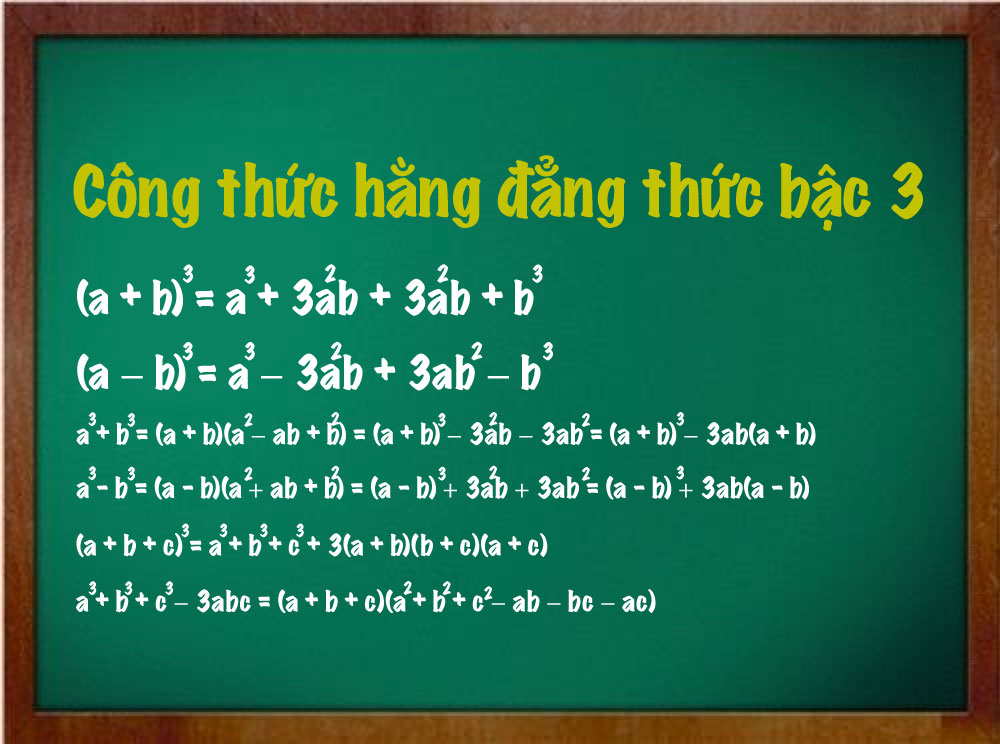


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Hằng đẳng thức mở rộng là những công thức toán học được mở rộng từ các hằng đẳng thức cơ bản, giúp giải quyết các bài toán phức tạp hơn liên quan đến khai triển biểu thức, rút gọn biểu thức và giải phương trình. Chúng thường xuất hiện trong chương trình toán học ở cấp THCS và THPT.
Tổng quát về hằng đẳng thức mở rộng
Các hằng đẳng thức cơ bản:
Các hằng đẳng thức mở rộng được xây dựng dựa trên các hằng đẳng thức cơ bản như: (a+b)² = a² + 2ab + b²; (a-b)² = a² - 2ab + b²; a² - b² = (a+b)(a-b); (a+b)³ = a³ + 3a²b + 3ab² + b³; (a-b)³ = a³ - 3a²b + 3ab² - b³. Hiểu rõ các hằng đẳng thức cơ bản là nền tảng để nắm vững hằng đẳng thức mở rộng.Hằng đẳng thức mở rộng thường gặp:
Một số hằng đẳng thức mở rộng thường gặp bao gồm: (a+b+c)² = a² + b² + c² + 2(ab+bc+ca); a³ + b³ + c³ - 3abc = (a+b+c)(a² + b² + c² - ab - bc - ca); aⁿ + bⁿ = (a+b)(aⁿ⁻¹ - aⁿ⁻²b + aⁿ⁻³b² - ... + bⁿ⁻¹), với n là số nguyên dương lẻ; aⁿ - bⁿ = (a-b)(aⁿ⁻¹ + aⁿ⁻²b + aⁿ⁻³b² + ... + bⁿ⁻¹), với n là số nguyên dương. Việc hiểu và áp dụng linh hoạt các hằng đẳng thức mở rộng giúp giải quyết nhanh chóng và chính xác các bài toán.Ứng dụng của hằng đẳng thức mở rộng:
Hằng đẳng thức mở rộng được ứng dụng rộng rãi trong nhiều lĩnh vực toán học như: phân tích đa thức thành nhân tử, giải phương trình, bất đẳng thức, tính toán nhanh... Việc thành thạo các hằng đẳng thức mở rộng giúp học sinh, sinh viên giải quyết các bài toán một cách hiệu quả hơn.Mẹo nhớ và áp dụng hằng đẳng thức mở rộng
Thường xuyên luyện tập:
Cách tốt nhất để nhớ và áp dụng thành thạo hằng đẳng thức mở rộng là thường xuyên luyện tập giải các bài tập đa dạng. Hãy bắt đầu từ các bài tập cơ bản rồi dần nâng cao độ khó.Tìm hiểu nguồn gốc:
Hiểu rõ nguồn gốc và cách chứng minh của các hằng đẳng thức mở rộng sẽ giúp bạn ghi nhớ lâu hơn và áp dụng linh hoạt hơn.Phân loại và tổng hợp:
Hãy sắp xếp và phân loại các hằng đẳng thức mở rộng theo từng nhóm để dễ dàng nhớ và tìm kiếm khi cần thiết. Việc lập mindmap cũng là một cách rất hữu hiệu.Xem thêm: duong trung truc la gi
Sản phẩm hữu ích: lay la so tu vi
Xem thêm: cake học tiếng anh
Sản phẩm liên quan: thay công tơ mét xe máy bao nhiêu tiền
Sản phẩm liên quan: chung minh tam giac can