Dãy Số Có Quy Luật Đặc Biệt

Mô tả sản phẩm

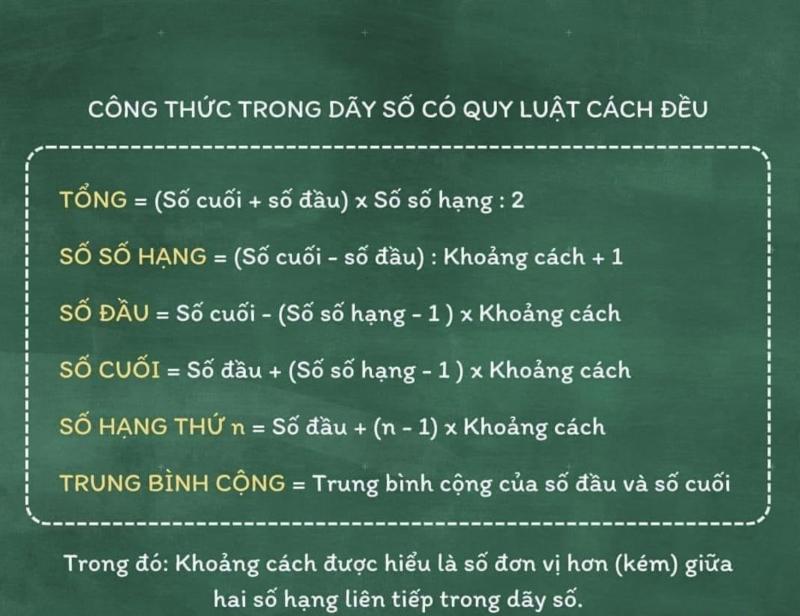
Dãy số có quy luật đặc biệt là những dãy số mà các số hạng được sắp xếp theo một quy luật nhất định, có thể là cộng, trừ, nhân, chia, hoặc kết hợp các phép tính đó. Việc tìm ra quy luật giúp chúng ta dự đoán được các số hạng tiếp theo trong dãy. Bài viết này sẽ giúp bạn hiểu rõ hơn về các loại dãy số có quy luật đặc biệt và cách tìm quy luật của chúng.

Các Loại Dãy Số Có Quy Luật Đặc Biệt

Dãy số cộng:

Đây là loại dãy số mà hiệu giữa hai số hạng liên tiếp luôn không đổi. Ví dụ: 2, 5, 8, 11, 14... (quy luật: cộng 3). Công thức tổng quát của dãy số cộng là: a_n = a₁ + (n-1)d, trong đó a_n là số hạng thứ n, a₁ là số hạng đầu tiên, và d là công sai (hiệu giữa hai số hạng liên tiếp).

Dãy số nhân:

Đây là loại dãy số mà thương giữa hai số hạng liên tiếp luôn không đổi. Ví dụ: 3, 6, 12, 24, 48... (quy luật: nhân 2). Công thức tổng quát của dãy số nhân là: a_n = a₁ * r^(n-1), trong đó a_n là số hạng thứ n, a₁ là số hạng đầu tiên, và r là công bội (thương giữa hai số hạng liên tiếp).

Dãy số Fibonacci:

Đây là một dãy số nổi tiếng, trong đó mỗi số hạng là tổng của hai số hạng trước đó. Ví dụ: 1, 1, 2, 3, 5, 8, 13... Dãy số Fibonacci có nhiều ứng dụng trong toán học và tự nhiên.

Dãy số hình học:

Dãy số hình học là một dãy số mà tỉ số giữa hai số hạng liên tiếp là hằng số. Ví dụ: 2, 4, 8, 16, 32...(quy luật: nhân 2).

Dãy số lập phương:

Dãy số này bao gồm các số là lập phương của các số tự nhiên. Ví dụ: 1, 8, 27, 64, 125... (1³, 2³, 3³, 4³, 5³...). Việc tìm ra quy luật của một dãy số có thể đòi hỏi sự quan sát, phân tích và suy luận logic. Tuy nhiên, bằng cách hiểu rõ các loại dãy số cơ bản và áp dụng các công thức, bạn sẽ có thể giải quyết được hầu hết các bài toán liên quan đến dãy số có quy luật đặc biệt. Hãy luyện tập thường xuyên để nâng cao kỹ năng của mình!

Sản phẩm liên quan: định lượng glucose trong máu cao

Sản phẩm hữu ích: 1 canh giờ bằng bao nhiêu tiếng

Xem thêm: chân chất thật thà

Xem thêm: 25% của 15 tấn là

Xem thêm: ví dụ về từ đơn