Công Thức Đạo Hàm Toán Học: Tổng Hợp Các Công Thức Quan Trọng

Mô tả sản phẩm

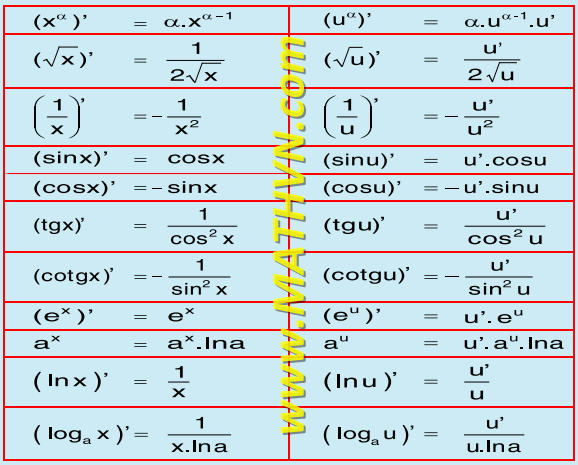
Công thức đạo hàm là nền tảng của phép tính vi phân, giúp tính toán tốc độ thay đổi của hàm số. Bài viết này sẽ tổng hợp các công thức đạo hàm quan trọng và thường gặp, giúp bạn nắm vững kiến thức này.

Đạo Hàm Của Các Hàm Số Cơ Bản

Đạo hàm của hàm hằng số:

Nếu f(x) = c (c là hằng số), thì f'(x) = 0.

Đạo hàm của hàm số lũy thừa:

Nếu f(x) = xⁿ (n là số thực), thì f'(x) = nx^n-1.

Đạo hàm của hàm số mũ:

Nếu f(x) = a^x (a > 0, a ≠ 1), thì f'(x) = a^xln(a). Đặc biệt, nếu f(x) = e^x, thì f'(x) = e^x.

Đạo hàm của hàm số logarit:

Nếu f(x) = log_a(x) (a > 0, a ≠ 1, x > 0), thì f'(x) = 1/(xln(a)). Đặc biệt, nếu f(x) = ln(x), thì f'(x) = 1/x.

Đạo hàm của hàm lượng giác:

* Nếu f(x) = sin(x), thì f'(x) = cos(x). * Nếu f(x) = cos(x), thì f'(x) = -sin(x). * Nếu f(x) = tan(x), thì f'(x) = sec²(x). * Nếu f(x) = cot(x), thì f'(x) = -csc²(x). * Nếu f(x) = sec(x), thì f'(x) = sec(x)tan(x). * Nếu f(x) = csc(x), thì f'(x) = -csc(x)cot(x).

Quy Tắc Đạo Hàm

Quy tắc tổng:

(f(x) + g(x))' = f'(x) + g'(x)

Quy tắc hiệu:

(f(x) - g(x))' = f'(x) - g'(x)

Quy tắc tích:

(f(x)g(x))' = f'(x)g(x) + f(x)g'(x)

Quy tắc thương:

(f(x)/g(x))' = [f'(x)g(x) - f(x)g'(x)] / [g(x)]² (với g(x) ≠ 0)

Quy tắc chuỗi:

Nếu y = f(u) và u = g(x), thì dy/dx = (dy/du)(du/dx) = f'(g(x))g'(x)

Sản phẩm liên quan: đơn vị đổi kg

Sản phẩm liên quan: xe đi từ bình dương về lagi

Xem thêm: chạy trốn với một con nhím