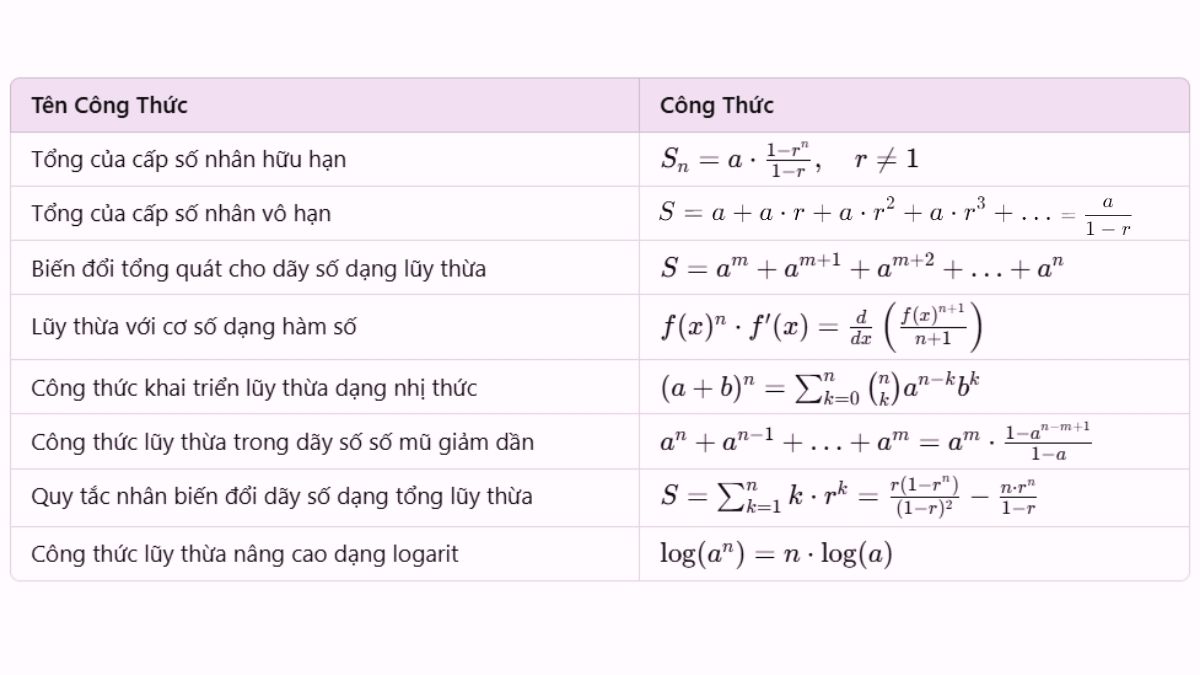
Công thức Lũy thừa Toán học

Mô tả sản phẩm

Bài viết này sẽ tổng hợp đầy đủ các công thức lũy thừa quan trọng trong toán học, giúp bạn nắm vững kiến thức và giải quyết các bài toán liên quan một cách dễ dàng. Chúng ta sẽ tìm hiểu từ những công thức cơ bản đến những công thức phức tạp hơn.

Các công thức lũy thừa cơ bản

Lũy thừa với số mũ tự nhiên

Công thức tính lũy thừa với số mũ tự nhiên n (n ≥ 1) của một số a được định nghĩa là tích của n thừa số a: aⁿ = a × a × ... × a (n thừa số). Ví dụ: 2³ = 2 × 2 × 2 = 8.

Lũy thừa với số mũ nguyên âm

Với a ≠ 0 và n là số nguyên dương, ta có: a^-n = 1/aⁿ. Ví dụ: 2^-3 = 1/2³ = 1/8.

Lũy thừa với số mũ bằng 0

Với a ≠ 0, ta có: a⁰ = 1.

Lũy thừa của một tích

(a × b)ⁿ = aⁿ × bⁿ. Ví dụ: (2 × 3)² = 2² × 3² = 4 × 9 = 36.

Lũy thừa của một thương

(a/b)ⁿ = aⁿ / bⁿ (với b ≠ 0). Ví dụ: (2/3)² = 2² / 3² = 4/9.

Lũy thừa của một lũy thừa

(a^m)ⁿ = a^{m × n}. Ví dụ: (2²)³ = 2^{2 × 3} = 2⁶ = 64.

Các công thức lũy thừa nâng cao

Lũy thừa với số mũ hữu tỉ

Nếu m, n là các số nguyên và n > 0 thì a^m/n = (a^1/n)^m = ⁿ√a^m (với a ≥ 0 nếu n chẵn).

Lũy thừa với số mũ vô tỉ

Lũy thừa với số mũ vô tỉ được định nghĩa thông qua giới hạn của dãy số. Ví dụ: a^π được định nghĩa là giới hạn của dãy a^r_n, trong đó r_n là một dãy số hữu tỉ hội tụ về π.

Ứng dụng của công thức lũy thừa

Công thức lũy thừa được ứng dụng rộng rãi trong nhiều lĩnh vực như: giải toán, vật lý, hóa học, kỹ thuật, tài chính,... Việc nắm vững các công thức lũy thừa là nền tảng quan trọng để học tốt các môn học này.

Sản phẩm hữu ích: lông chó mực có tác dụng gì

Xem thêm: các công thức hoá học cần nhớ

Sản phẩm hữu ích: túi ngủ mùa đông cho bé