Công thức Nhị Thức Newton
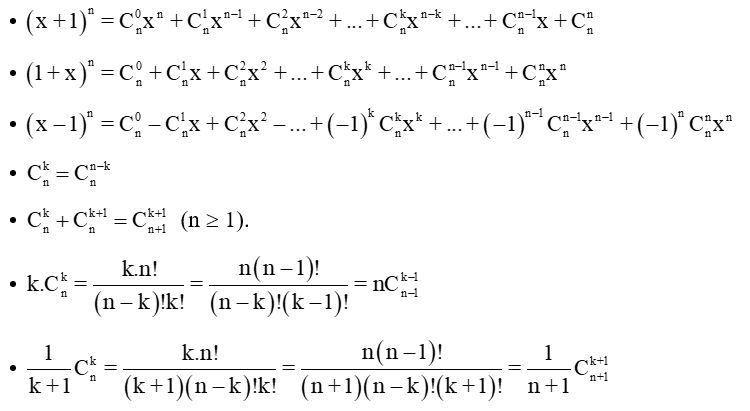

Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Công thức nhị thức Newton là một công thức toán học quan trọng cho phép bạn khai triển một biểu thức dạng (a + b)n thành một tổng các số hạng. Nó được sử dụng rộng rãi trong nhiều lĩnh vực, từ đại số đến xác suất thống kê.
Công thức tổng quát
Định nghĩa
Công thức nhị thức Newton cho phép khai triển (a + b)n như sau: (a + b)n = Σk=0n (n k) an-k bk trong đó: * n là một số nguyên không âm. * k là chỉ số chạy từ 0 đến n. * (n k) là tổ hợp chập k của n phần tử, được tính bằng công thức: (n k) = n! / (k! (n-k)!) với n! là giai thừa của n (n! = n*(n-1)*(n-2)*...*2*1).Ví dụ minh họa
Hãy khai triển (x + y)3 sử dụng công thức nhị thức Newton: (x + y)3 = (3 0)x3y0 + (3 1)x2y1 + (3 2)x1y2 + (3 3)x0y3 = x3 + 3x2y + 3xy2 + y3Ứng dụng của công thức nhị thức Newton
Công thức nhị thức Newton có nhiều ứng dụng quan trọng trong toán học và các lĩnh vực liên quan, bao gồm:Trong Đại số
* Khai triển các biểu thức dạng (a + b)n một cách nhanh chóng và chính xác. * Tính toán các giá trị gần đúng của các biểu thức phức tạp.Trong Xác suất và Thống kê
* Tính toán xác suất trong phân phối nhị thức. * Xây dựng các mô hình thống kê.Trong Giải tích
* Sử dụng trong khai triển chuỗi Taylor và Maclaurin.Tổng kết
Công thức nhị thức Newton là một công cụ mạnh mẽ và hữu ích trong nhiều lĩnh vực toán học. Hiểu rõ công thức và cách áp dụng nó sẽ giúp bạn giải quyết nhiều bài toán phức tạp một cách hiệu quả.Sản phẩm liên quan: tổng hợp kiến thức toán hình thi vào lớp 10
Sản phẩm liên quan: khối nón
Sản phẩm hữu ích: cắt nhung hươu có đau không