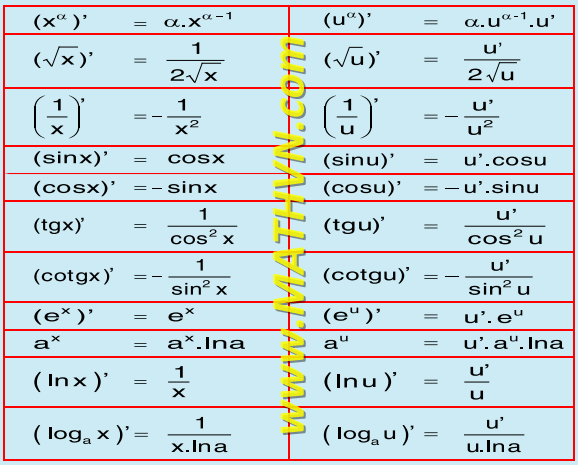
Công thức đạo hàm cơ bản

Mô tả sản phẩm

Bạn đang tìm kiếm các công thức đạo hàm cơ bản để phục vụ cho việc học tập và giải toán? Bài viết này sẽ tổng hợp đầy đủ và chi tiết các công thức đạo hàm quan trọng nhất, giúp bạn nắm vững kiến thức và áp dụng hiệu quả. Chúng ta sẽ cùng tìm hiểu các công thức đạo hàm của các hàm số cơ bản cũng như các quy tắc đạo hàm quan trọng.

Đạo hàm của các hàm số cơ bản

Hàm số hằng

Nếu f(x) = c (c là hằng số) thì f'(x) = 0

Hàm số lũy thừa

Nếu f(x) = xⁿ (n là số thực) thì f'(x) = nx^n-1

Hàm số mũ

Nếu f(x) = a^x (a > 0, a ≠ 1) thì f'(x) = a^xln(a)

Đặc biệt: Nếu f(x) = e^x thì f'(x) = e^x

Hàm số logarit

Nếu f(x) = log_ax (a > 0, a ≠ 1) thì f'(x) = 1/(xln(a))

Đặc biệt: Nếu f(x) = ln(x) thì f'(x) = 1/x

Hàm số lượng giác

Nếu f(x) = sin(x) thì f'(x) = cos(x)

Nếu f(x) = cos(x) thì f'(x) = -sin(x)

Nếu f(x) = tan(x) thì f'(x) = 1/cos²(x)

Nếu f(x) = cot(x) thì f'(x) = -1/sin²(x)

Các quy tắc đạo hàm

Quy tắc đạo hàm của tổng, hiệu

(f(x) ± g(x))' = f'(x) ± g'(x)

Quy tắc đạo hàm của tích

(f(x)g(x))' = f'(x)g(x) + f(x)g'(x)

Quy tắc đạo hàm của thương

(f(x)/g(x))' = (f'(x)g(x) - f(x)g'(x)) / (g(x))² (với g(x) ≠ 0)

Quy tắc đạo hàm hàm hợp

Nếu y = f(u) và u = g(x) thì dy/dx = (dy/du)(du/dx)

Xem thêm: những bài thơ hay về họp lớp

Sản phẩm hữu ích: bánh tráng tiếng anh là gì

Sản phẩm hữu ích: cuối đường sinh đạo có hình tam giác