Biến cố và Xác suất của Biến cố

Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
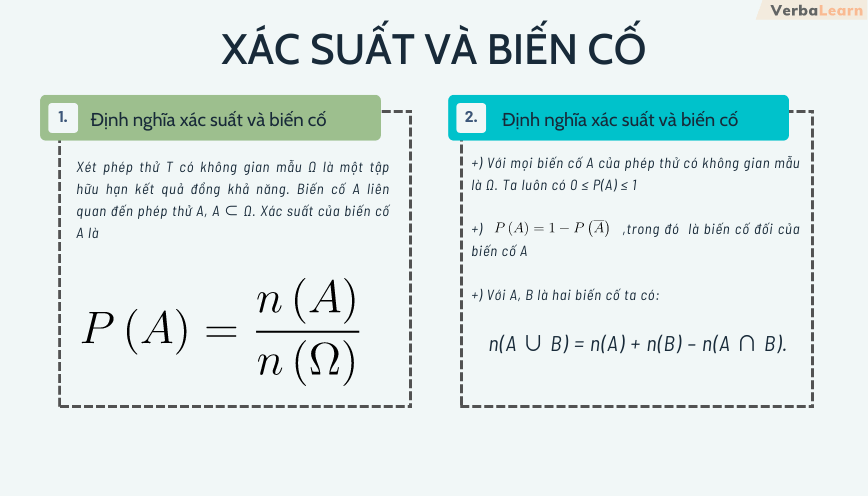
Biến cố và xác suất của biến cố là hai khái niệm cơ bản trong lý thuyết xác suất, giúp chúng ta mô hình hóa và dự đoán kết quả của các hiện tượng ngẫu nhiên. Xác suất của một biến cố thể hiện khả năng xảy ra của biến cố đó, thường được biểu diễn bằng một số từ 0 đến 1. Một biến cố có xác suất 0 là biến cố không thể xảy ra, trong khi biến cố có xác suất 1 là biến cố chắc chắn xảy ra.
Khái niệm Biến cố
Định nghĩa Biến cố
Trong toán học, một biến cố là một tập hợp con của không gian mẫu. Không gian mẫu là tập hợp tất cả các kết quả có thể xảy ra của một phép thử ngẫu nhiên. Ví dụ, nếu ta tung một đồng xu, không gian mẫu là {S, N} (S: sấp, N: ngửa). Một biến cố A có thể là "xuất hiện mặt sấp", tức là A = {S}.
Các loại biến cố
Có nhiều loại biến cố khác nhau, bao gồm:
- Biến cố chắc chắn: Biến cố luôn xảy ra (xác suất bằng 1).
- Biến cố không thể: Biến cố không bao giờ xảy ra (xác suất bằng 0).
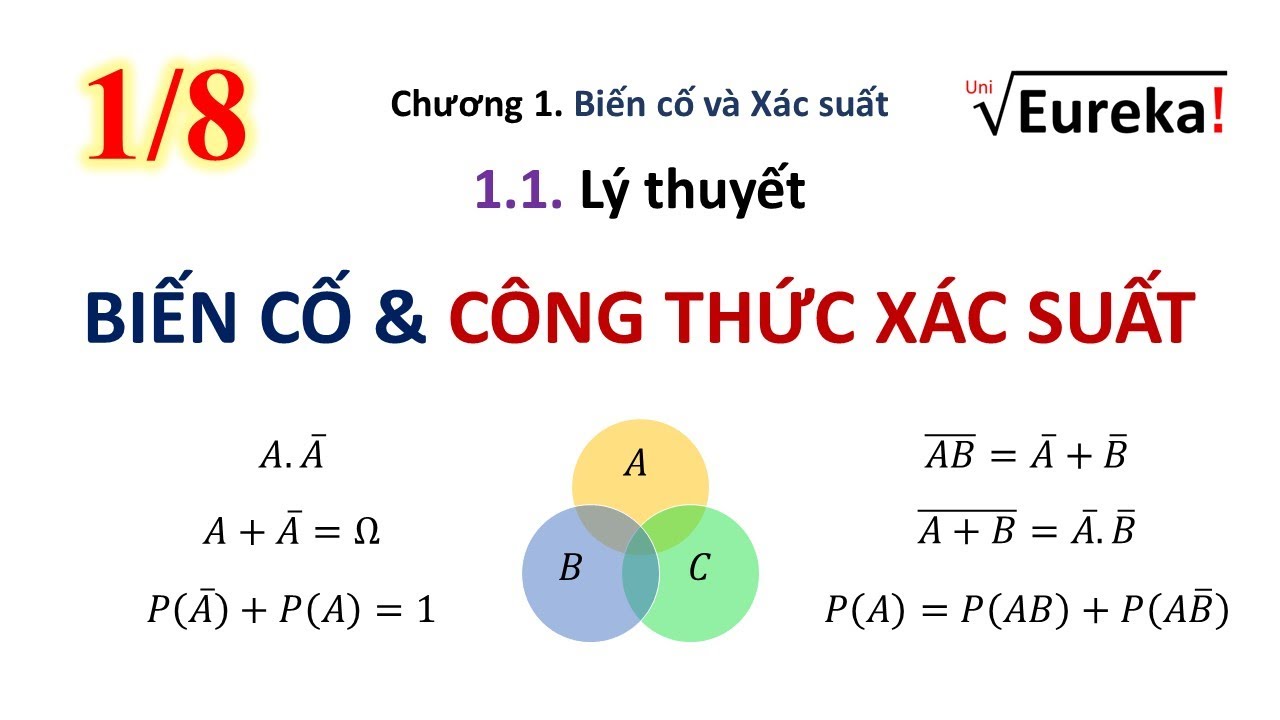
- Biến cố đối: Biến cố đối của biến cố A là biến cố không xảy ra A, ký hiệu là Ac hoặc Ā.
- Biến cố xung khắc (biến cố loại trừ): Hai biến cố không thể xảy ra đồng thời.
- Biến cố độc lập: Xác suất xảy ra của một biến cố không bị ảnh hưởng bởi việc xảy ra hay không xảy ra của biến cố khác.
Xác suất của Biến cố
Tính xác suất
Xác suất của một biến cố A, ký hiệu là P(A), được định nghĩa là tỷ số giữa số kết quả thuận lợi cho A và tổng số kết quả có thể xảy ra trong không gian mẫu. Nếu không gian mẫu hữu hạn và các kết quả có thể xảy ra có cùng khả năng, thì:
P(A) = (Số kết quả thuận lợi cho A) / (Tổng số kết quả có thể xảy ra)
Ví dụ: Xác suất xuất hiện mặt sấp khi tung một đồng xu cân đối là P(S) = 1/2.
Các quy tắc tính xác suất
Một số quy tắc quan trọng khi tính xác suất bao gồm:
- Quy tắc cộng: P(A ∪ B) = P(A) + P(B) - P(A ∩ B) (cho hai biến cố A và B bất kỳ).
- Quy tắc nhân: P(A ∩ B) = P(A) * P(B) (cho hai biến cố A và B độc lập).
- Xác suất của biến cố đối: P(Ac) = 1 - P(A).
Hiểu rõ về biến cố và xác suất của biến cố là nền tảng quan trọng để ứng dụng trong nhiều lĩnh vực như thống kê, kinh tế, kỹ thuật, và đời sống hàng ngày.
Sản phẩm liên quan: có mẹ nào cho con uống b1 chưa
Sản phẩm liên quan: hình nền hoa nhài
Sản phẩm liên quan: ô nhiễm tiếng ồn tiếng anh